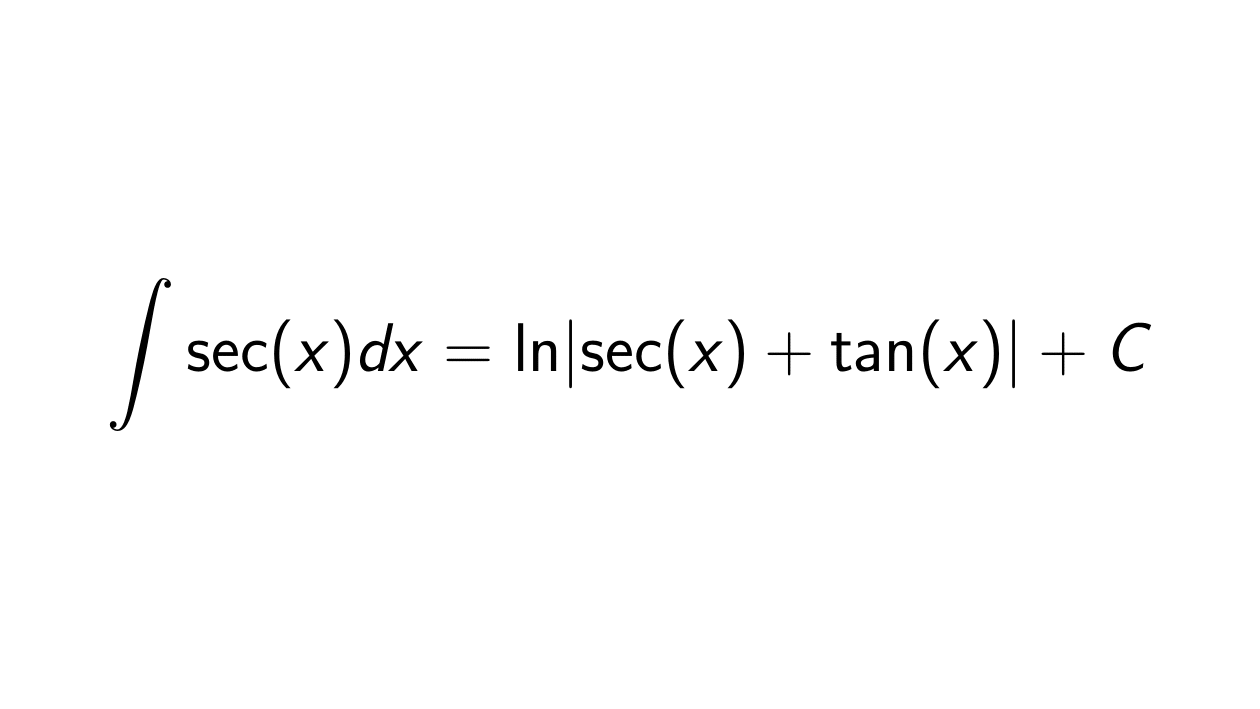Proof. This integral is more difficult to approach directly. We need to multiply \sec(x) with the fraction \frac{\sec(x) + \tan(x)}{\sec(x) + \tan(x)}. So we need to calculate the next integral:
\begin{align*}
\int \sec(x) dx = \int \frac{\sec(x)(\sec(x) + \tan(x))}{\sec(x) + \tan(x)} dx.
\end{align*}\begin{align*}
\frac{du}{dx} = \sec(x)\tan(x) + \tan^2(x) \iff du = (\sec(x)\tan(x) + \tan^2(x))dx.
\end{align*}\begin{align*}
\int \sec(x) dx &= \int \frac{\sec(x)(\sec(x) + \tan(x))}{\sec(x) + \tan(x)} dx \\
&= \int \frac{\sec(x)\tan(x) + \tan^2(x)}{\sec(x) + \tan(x)} dx \\
&= \int \frac{du}{u} \\
&= \ln \lvert u \rvert + C \\
&= \ln \lvert \sec(x) + \tan(x) \rvert + C.
\end{align*}