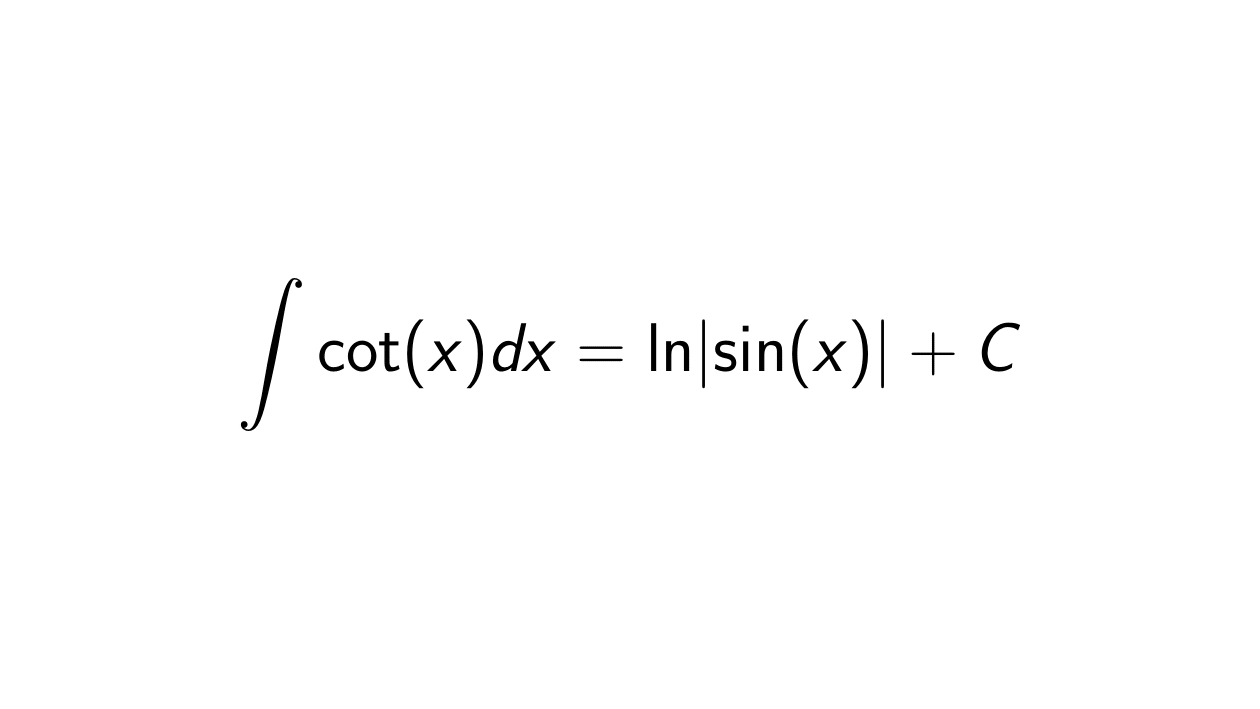Proof. By definition, we have that \cot(x) = \frac{1}{\tan(x)} = \frac{\cos(x)}{\sin(x)}. So:
\begin{align*}
\int \cot(x) dx = \int \frac{1}{\tan(x)} dx = \int \frac{\cos(x)}{\sin(x)} dx.
\end{align*}\begin{align*}
\frac{d}{dx} u = \cos(x) \iff du = \cos(x)dx.
\end{align*}\begin{align*}
\int \cot(x) dx = \int \frac{1}{\tan(x)} dx
&= \int \frac{\cos(x)}{\sin(x)} dx \\
&= \int \frac{1}{u} du \\
&= \ln \lvert u \rvert + C \\
&= \ln \lvert \sin(x) \rvert + C \quad \text{since } u = \sin(x).
\end{align*}