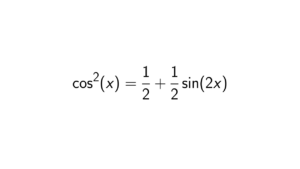Proof. For simplicity, we start with n = 2. Let A,B \in M_n(R) such that
A = \begin{pmatrix}
r_{11} & 0 \\
0 & 0
\end{pmatrix} \text{ and } \begin{pmatrix}
0 & r_{12} \\
0 & 0
\end{pmatrix} AB = \begin{pmatrix}
r_{11} & 0 \\
0 & 0
\end{pmatrix}\begin{pmatrix}
0 & r_{12} \\
0 & 0
\end{pmatrix} = \begin{pmatrix}
0 & r_{11}r_{12} \\
0 & 0
\end{pmatrix} BA = \begin{pmatrix}
0 & r_{12} \\
0 & 0
\end{pmatrix}\begin{pmatrix}
r_{11} & 0 \\
0 & 0
\end{pmatrix} = \begin{pmatrix}
0 & 0 \\
0 & 0
\end{pmatrix}.Now, we take dimension n \geq 3. Let A be a matrix where the coefficient r_{11} \in R is the first row and first column position of A and zero elsewhere. Further, let B be a matrix where the coefficient r_{12} \in R is the first row and second column position of B and zero elsewhere. Let r_{11}r_{12} \neq 0 and r_{12}r_{11} \neq 0. Then if we multiply A and B, then for AB, we have on the first row and second column position the value r_{11}r_{12} and zero everywhere, and for BA, we have everywhere zero. This proves that AB \neq BA, and therefore, the matrix ring is not commutative for dimensions greater or equal than 2.