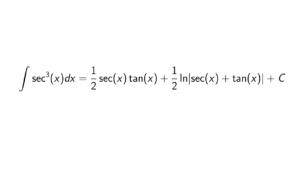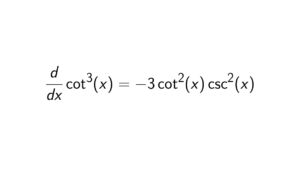How to prove that if R[x] is a P.I.D. and R commutative then R is a field

We will use the fact that every prime ideal in a P.I.D. is a maximal ideal, which we have proved here.

Prove that if R[x] is a P.I.D. and R commutative then R is a field

Proof: given R[x] is a principal ideal domain. We have proven here R is an integral domain since it is a subring of R[x]. Further, we have that R[x]/(x) \cong R and since R is an integral domain, we do know that (x) is a prime ideal. But every prime ideal is a maximal ideal and therefore R[x]/(x) must be a field, which implicates that R is a field.