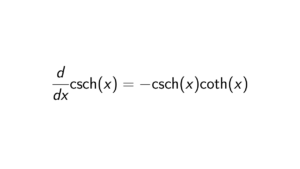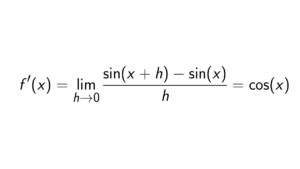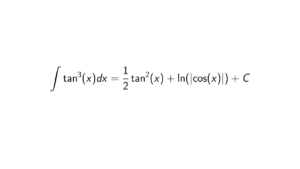Blog

Prove that $(2,x)$ is not a principal ideal of $\mathbb{Z}[x]$

Proof. Assume by contradiction that $(2,x)$ is a principal ideal. Then $(2,x) = (f(x))$, where $f(x) \in \mathbb{Z}[x]$. Say we have $2 \in (f(x))$. Then by the definition of an ideal, we have that $2 = f(x)g(x)$ for some $g(x) \in \mathbb{Z}[x]$. By some basic calculus and that $\mathbb{Z}[x]$ is an integral domain, we have that $deg(f(x)g(x)) = deg(f(x)) + deg(g(x))$. So we know $2 = f(x)g(x)$ possible if both $f(x)$ and $g(x)$ are constants. This implies that $f(x),g(x) \in \{\pm 1, \pm 2\}$. We see the two different situations:

1. Assume that $f(x) = \pm 1$. Then this implies that $(f(x)) = \mathbb{Z}[x]$, which is not a proper ideal.
2. Assume that $f(x) = \pm 2$. Then we have that if $x \in (f(x))$, then $x = 2\cdot g(x)$. This implies that $g(x) = \frac{1}{2}x$, which is impossible since $g(x) \in \{\pm 1, \pm 2\}$ and secondly $\frac{1}{2} \not \in \mathbb{Z}$.

So $(2,x)$ is not a principal ideal of $\mathbb{Z}[x]$, which completes the proof.

Note that with the proof above, we also proved that $\mathbb{Z}[x]$ is not a PID.