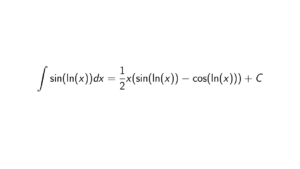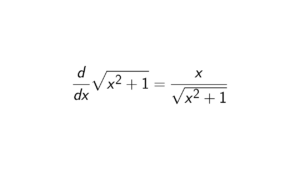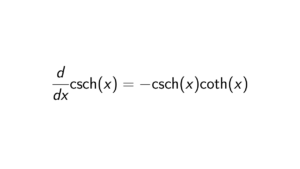Let p and q be distinct primes. If x \equiv a \ (\text{mod } p) and x \equiv a \ (\text{mod } q), then x \equiv a \ (\text{mod } pq).
Proof. Since
x \equiv a \ (\text{mod } p) and
x \equiv a \ (\text{mod } q), we have that
\begin{align*}
p &\mid (x - a) \\
q &\mid (x - a).
\end{align*}
By the fact that each integer has a unique prime factorization, we see that
\begin{align*}
x - a = \sum_{i = 1}^l r_i^{m_i}
\end{align*}
where
r_i are distinct primes and
p = r_j and
q = r_k for some
i \in \{1,2,\ldots,l\}. Therefore, we get
\begin{align*}
pq \mid (x - a).
\end{align*}
which implies that
x \equiv a \ (\text{mod } pq).