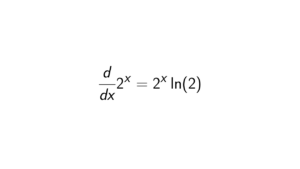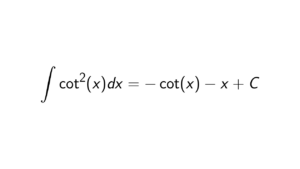Blog

What are the normal subgroups of S3?

The normal subgroups of S3 are the identity group, \{e,(123),(132)\}, and S3 itself. To prove this, a subgroup of S_3, say N, is a normal subgroup of G if gNg^{-1} \in N for all g \in G.

Proof. We start with the identity group \{e\}. This is straightforward as we get geg^{-1} = gg^{-1} = e \in \{e\} for all g \in G. Therefore \{e\} is a normal subgroup. Next, we will look at the subgroups of order 2, i.e., \{e, (12)\}, \{e, (13)\} and \{e, (23)\}. We see that none of them are normal subgroups: 
\begin{align*}
(13)(12)(31) &= (23) \not \in \{e,(12)\} \\ 
(23)(13)(32) &= (12) \not \in \{e,(13)\} \\ 
(12)(23)(21) &= (13) \not \in \{e,(23)\} \\ 
\end{align*}
Our last subgroup which we need to check is the subgroup of order 3, i.e., \{e,(123),(132)\}. This is a normal subgroup because: 
\begin{align*}
e(123)e &= (123) \\ 
(12)(123)(21) &= (132) \\ 
(13)(123)(31) &= (132) \\ 
(23)(123)(32) &= (132) \\ 
(123)(123)(321) &= (123) \\ 
(132)(123)(231) &= (123) \\ 
\end{align*}
and 
\begin{align*}
e(132)e &= (132) \\ 
(12)(132)(21) &= (123) \\ 
(13)(132)(31) &= (123) \\ 
(23)(132)(32) &= (123) \\ 
(123)(132)(321) &= (132) \\ 
(132)(132)(231) &= (132) \\ 
\end{align*}
As S_3 is closed under composite, we have that S_3 is a normal subgroup itself. So we have proved that the identity group, the alternating group of degree 3, and S3 itself are the normal subgroups of S3.
Tags: ,

Leave a Reply