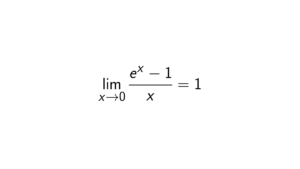The centralizer of a group center is the group itself
We want to prove the following statement: C_G(Z(G)) = G.
Proof. “\subseteq“: This one is straightforward.
“\supseteq“: Let g \in G. Then by definition of the group center, we have gz = zg for all z \in Z(G). Now, we have that gz = zg for all z \in Z(G) if and only if z = gzg^{-1} for all z \in Z(G), which means that g \in C_G(Z(G)).