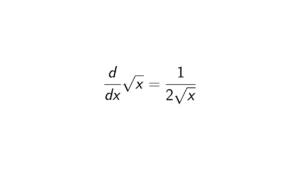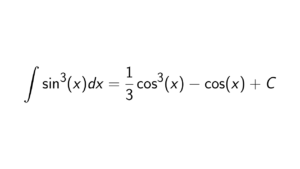Show that Z is a group under addition

The set of integers is a group under addition. To show why

\mathbb{Z}

is a group under addition, we need to verify that the elements of

\mathbb{Z}

are associative under addition, that there exists an identity element in

\mathbb{Z}

and that for all elements in

\mathbb{Z}

there exists an inverse.

Proof.

Associativity: let

a,b,c \in \mathbb{Z}

. Then

\begin{align*} (a + b) + c = a + b + c = a + (b + c) \\ \end{align*}

+

is associative.

Identity: let

a \in \mathbb{Z}

. Then let

e

be an element of

\mathbb{Z}

such that

a + e = e + a = a

. Logically, this means that

e = 0

. So

0

is the identity element of

\mathbb{Z}

under addition.

Inverse: let

a \in \mathbb{Z}

. Then there exist an element

a^{-1}

such that

a + a^{-1} = a^{-1} + a = e

. We see that

a^{-1} = -a

and therefore

-a

is the inverse element of

a

.

We have proved all three properties; therefore, the ordered pair

(\mathbb{Z}, +)

is a group.

The set of integers is a commutative group too under addition. This is easy to verify.