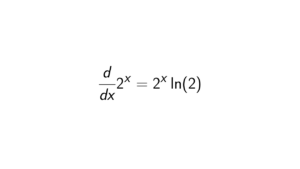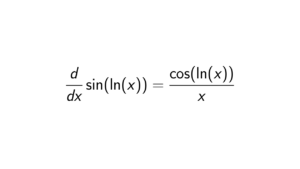Prove that the multiplicative groups \mathbb{R}-{0} and \mathbb{C}-{0} are not isomorphic
Proof. Assume that
\mathbb{R}-{0} is isomorphic to
\mathbb{C}-{0}. Then there exists a mapping
\begin{align*}
\phi: \mathbb{C}-{0} \longrightarrow \mathbb{R}-{0}
\end{align*}
which is bijective and is a group homomorphism. By the definition of a group homomorphism, we have that
\phi(1) = 1. We can also rewrite that as:
\begin{align*}
1 = \phi(1) = \phi((-1)(-1)) = \phi(-1)\phi(-1) = \phi(-1)^2.
\end{align*}
Since
\phi is injective, it must hold that
\phi(-1) = -1. Again, we can rewrite that as:
\begin{align*}
-1 = \phi(-1) = \phi(i^2) = \phi(i)^2.
\end{align*}
So this means that
\phi(i)^2 \in \mathbb{R}^{\times}. But that is not possible since
\phi(i)^2 must be positive number in
\mathbb{R}^{\times}, and therefore
\phi(i)^2 \not \in \mathbb{R}^{\times}. A contradiction.
So, the multiplicative groups
\mathbb{R}-{0} and
\mathbb{C}-{0} are not isomorphic.