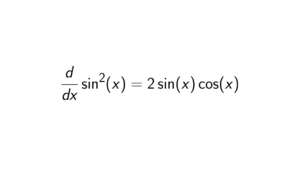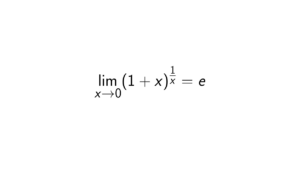Prove that the group
A_4 is not abelian.
Proof. First of all, the alternating group of degree 4 is defined as:
\begin{align*}
A_4 = \{1,(123),(124),(132),(134),(142),(143),(234),(243),(12)(34),(13)(24),(14)(23)\}.
\end{align*}
To show that
A_4 is not abelian, we need to find a counterexample. That is, we need to find
\sigma, \tau \in A_4 such that
\sigma\tau \neq \tau\sigma. So, let
\sigma = (123), \tau = (13)(24) \in A_4. Then
\begin{align*}
(123)(13)(24) = 1
\end{align*}
and
\begin{align*}
(13)(24)(123) = (142).
\end{align*}
But
(123)(13)(24) \neq (13)(24)(123), so
A_4 is not abelian.