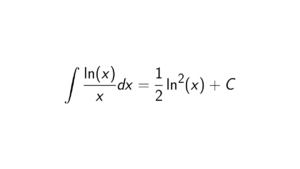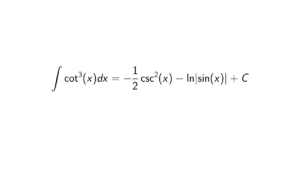Prove that the additive groups Z and Q are not isomorphic

Prove that the additive groups $\mathbb{Z}$ and $\mathbb{Q}$ are not isomorphic.

Proof. Assume that

\mathbb{Z}

and

\mathbb{Q}

are isomorphic. Then there exists a mapping

\begin{align*} \phi: \mathbb{Q} \longrightarrow \mathbb{Z} \end{align*}

such that

\phi

is bijective and is a group homomorphism. This also means that there exists an element

q \in \mathbb{Q}

such that

\phi(q) = 1_{\mathbb{Z}}

(note that

0

is the identity element and not

1

since we are working with additivity groups). So we have the following:

\begin{align*} \phi(q) &= \phi(q/2 + q/2) \\ &= \phi(q/2) + \phi(q/2), \quad \text{by group homomorphism} \\ &= 2\phi(q/2). \end{align*}

This means we have that

2\phi(q/2) = 1_{\mathbb{Z}}

, which implies that

\phi(q/2) = 1/2

. But

1/2 \not \in \mathbb{Z}

, so we have a contradiction. Therefore, the additive groups

\mathbb{Z}

and

\mathbb{Q}

are not isomorphic.