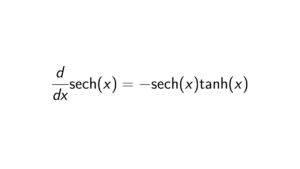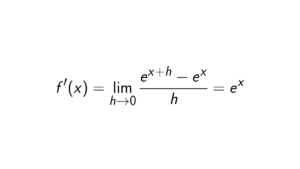Prove that aH = bH iff b^-1a in H

Let

H

be a subgroup of

G

and

a,b \in G

. Then

aH = bH

if and only if

b^{-1}a \in H

.

Proof. This is a straightforward proof. We have that

aH = bH

. Multiplying both sides with

b^{-1}

, we get

b^{-1}(aH) = b^{-1}(bH)

, which implies that

b^{-1}aH = H

. This means that

b^{-1}a

is an element of

H

, because subgroups contain the identity element. We could write this in summary:

\begin{align*} aH = bH &\iff b^{-1}(aH) = b^{-1}(bH) \\ &\iff b^{-1}aH = H \\ &\iff b^{-1}a \in H. \end{align*}