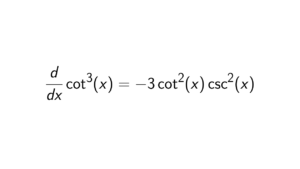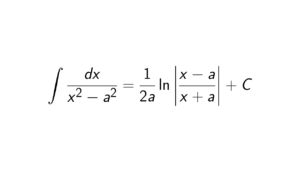Proof. We want to show that (R, \times) is not a group under multiplication. Let r \in \mathbb{R}.
Associativity is easily shown by the definition of \mathbb{R}. Further, we know that the identity element of \mathbb{R} is 1 since r \times 1 = 1 \times r = r.
Lastly, assuming by contradiction, we want to show that each element of \mathbb{R} has an inverse. All elements of \mathbb{R} do have an inverse, but zero doesn’t. In other words, there exist no r \in \mathbb{R} such that:
\begin{align*}
0 \times r = 1,
\end{align*}