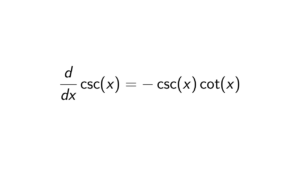If G/Z(G) is cyclic, then G is abelian.
Proof. Recall that that center of
G is defined as
\begin{align*}
Z(G) = \{z \in G \ | \ \forall g \in G, gz = zg\}.
\end{align*}
We have that
G/Z(G) is cyclic, so there exists an
x \in G such that
\begin{align*}
G/Z(G) = \langle xZ(G) \rangle
\end{align*}
where
x is the representative of the coset
xZ(G).
Let
g \in G. Then
gZ(G) = (xZ(G))^m = x^mZ(G) for some
m \in \mathbb{Z}, where the second equality is proven
here because
Z(G) is a normal subgroup of
G. Further,
we know that aH = bH if and only if b^{-1}a \in H, where
a,b \in G and
H is a subgroup of
G. So since
gZ(G) = x^mZ(G), we have that
(x^m)^{-1}g \in Z(G). Therefore, there exists an
z \in Z(G) such that
(x^m)^{-1}g = z if and only if
g = zx^m.
After seeing the above, we can finally prove that
G is abelian. Take
g_1,g_2 \in G such that
g_1 = x^kz_1 and
g_2 = x^lz_2 where
k,l \in \mathbb{Z} and
z_1,z_2 \in Z(G). So we get
\begin{align*}
g_1g_2 &= x^kz_1x^lz_2 \\
&= x^kx^lz_1z_2 \quad \text{because } z_1x^l = x^lz_1 \text{ as } z_1 \in Z(G)\\
&= x^{k + l}z_1z_2 \\
&= x^lx^kz_1z_2 \\
&= x^lx^kz_2z_1 \quad \text{because } z_1z_2 = z_2z_1 \text{ as } z_1,z_2 \in Z(G) \\
&= x^lz_2x^kz_1 \quad \text{because } x^kz_2 = z_2x^k \text{ as } z_2 \in Z(G) \\
&= g_2g_1,
\end{align*}
where we have proven that
G is abelian.