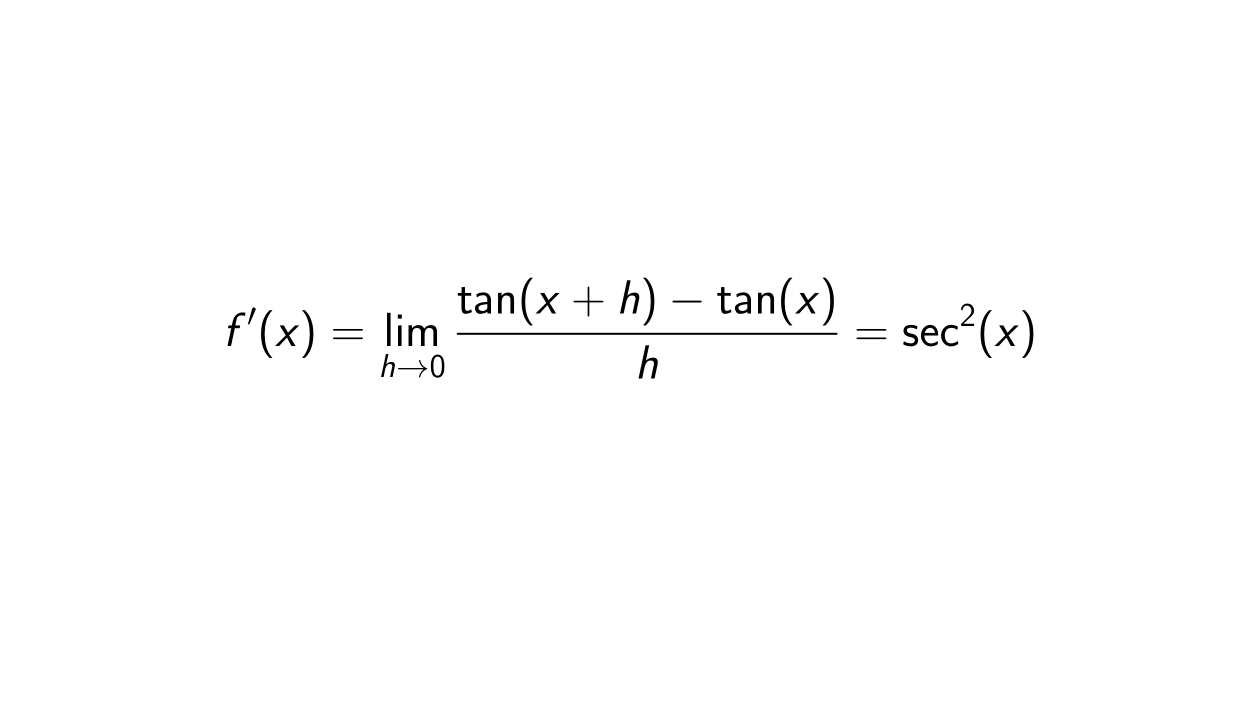Using the first principle of derivatives, we will prove the derivative of a tangent, or in other words, that the derivative
\tan(x) is
1/\cos^2(x).
Proof. Let
f(x) = \tan(x) = \frac{\sin(x)}{\cos(x)}. Then
\begin{align*}
f'(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\
&= \lim_{h \rightarrow 0} \frac{\tan(x + h) - \tan(x)}{h} \\
&= \lim_{h \rightarrow 0} \frac{\frac{\sin(x + h)}{\cos(x + h)} - \frac{\sin(x)}{\cos(x)}}{h} \\
&= \lim_{h \rightarrow 0} \frac{\frac{\sin(x + h)\cos(x) - \cos(x + h)\sin(x)}{\cos(x + h)\cos(x)}}{h}
\end{align*}
We will use the next identity:
\begin{equation*}
\sin(x - y) = \sin(x)\cos(y) - \cos(x)\sin(y).
\end{equation*}
This would imply for us that
\begin{equation*}
\sin(x + h)\cos(x) - \cos(x + h)\sin(x) = \sin(x + h - x) = \sin(h).
\end{equation*}
Therefore we get
\begin{align*}
\lim_{h \rightarrow 0} \frac{\frac{\sin(h)}{\cos(x + h)\cos(x)}}{h} = \lim_{h \rightarrow 0} \frac{\sin(h)}{h} \cdot \lim_{h \rightarrow 0} \frac{1}{\cos(x + h)\cos(x)}
\end{align*}
We do have know that
\lim_{h \rightarrow 0} \frac{\sin(h)}{h} = 1 from
this article. So continuing where we left:
\begin{align*}
\lim_{h \rightarrow 0} \frac{1}{\cos(x + h)\cos(x)} = \frac{1}{\cos(x)\cos(x)} = \frac{1}{\cos^2(x)} = \sec^2(x)
\end{align*}
Therefore, we get
f'(x) = \frac{1}{\cos^2(x)} = \sec^2(x).