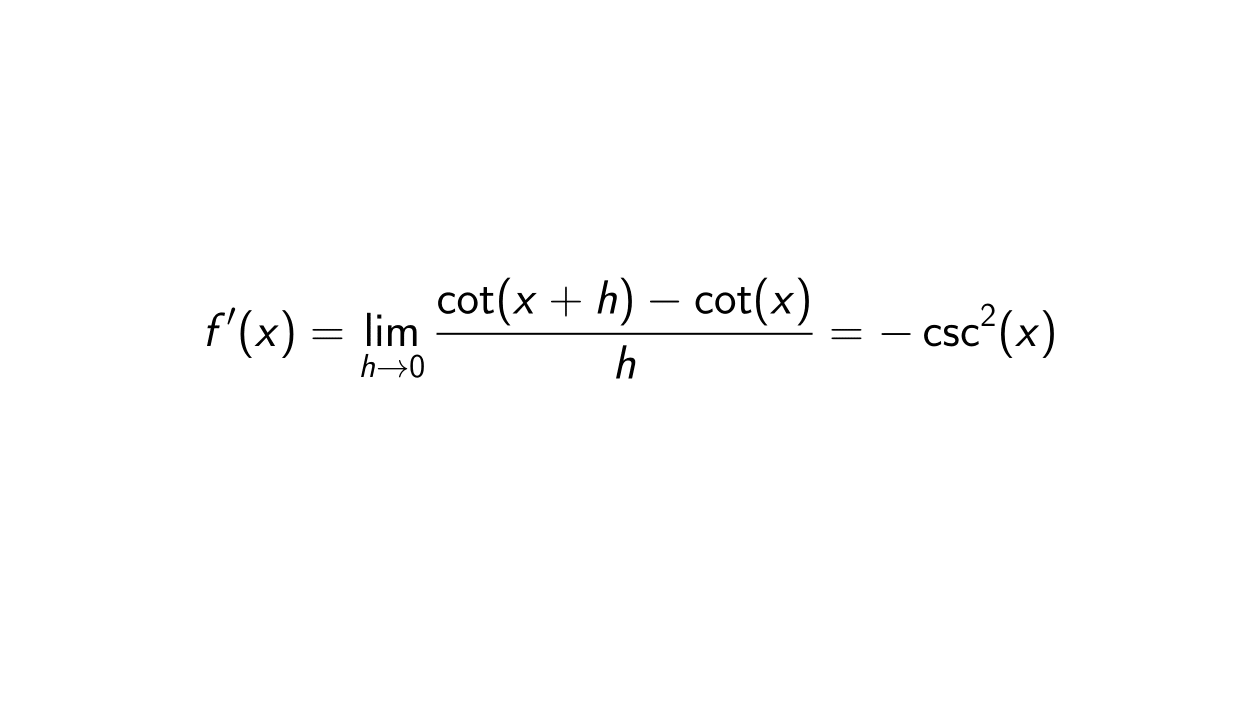Derivative of cot(x) using First Principle of Derivatives

Derivative of cot(x)

Using the First Principle of Derivatives, we will prove that the derivative of

\cot(x)

is equal to

-1/\sin^2(x)

. The derivative of cotangent is easier to prove if we take its identity, which is the inverse of the tangent.

Proof. Let

f(x) = \cot(x) = \frac{1}{\tan(x)} = \frac{\cos(x)}{\sin(x)}

. Then

\begin{align*} f'(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\cot(x + h) - \cot(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{\cos(x + h)}{\sin(x + h)} - \frac{\cos(x)}{\sin(x)}}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{\cos(x + h)\sin(x) - \sin(x + h)\cos(x)}{\sin(x + h)\sin(x)}}{h} \end{align*}

We will take the following identity

\begin{align*} \sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B). \end{align*}

Applying that to our case, then we get the following equality

\begin{align*} \cos(x + h)\sin(x) - \sin(x + h)\cos(x) = \sin(-h). \end{align*}

Since

\lim_{h \rightarrow 0} \frac{\sin(-h)}{h} = -\lim_{h \rightarrow 0} \frac{\sin(h)}{h} = -1

which we have seen here, we get:

\begin{align*} \lim_{h \rightarrow 0} \frac{\frac{\sin(-h)}{\sin(x + h)\sin(x)}}{h} &= \lim_{h \rightarrow 0} \frac{\sin(-h)}{h} \cdot \lim_{h \rightarrow 0} \frac{1}{\sin(x + h)\sin(x)} \\ &= - \lim_{h \rightarrow 0} \frac{1}{\sin(x + h)\sin(x)} \\ &= - \frac{1}{\sin^2(x)} \\ &= - \csc^2(x). \end{align*}

Therefore, we have that

f'(x) = - \frac{1}{\sin^2(x)} = -\csc^2(x)