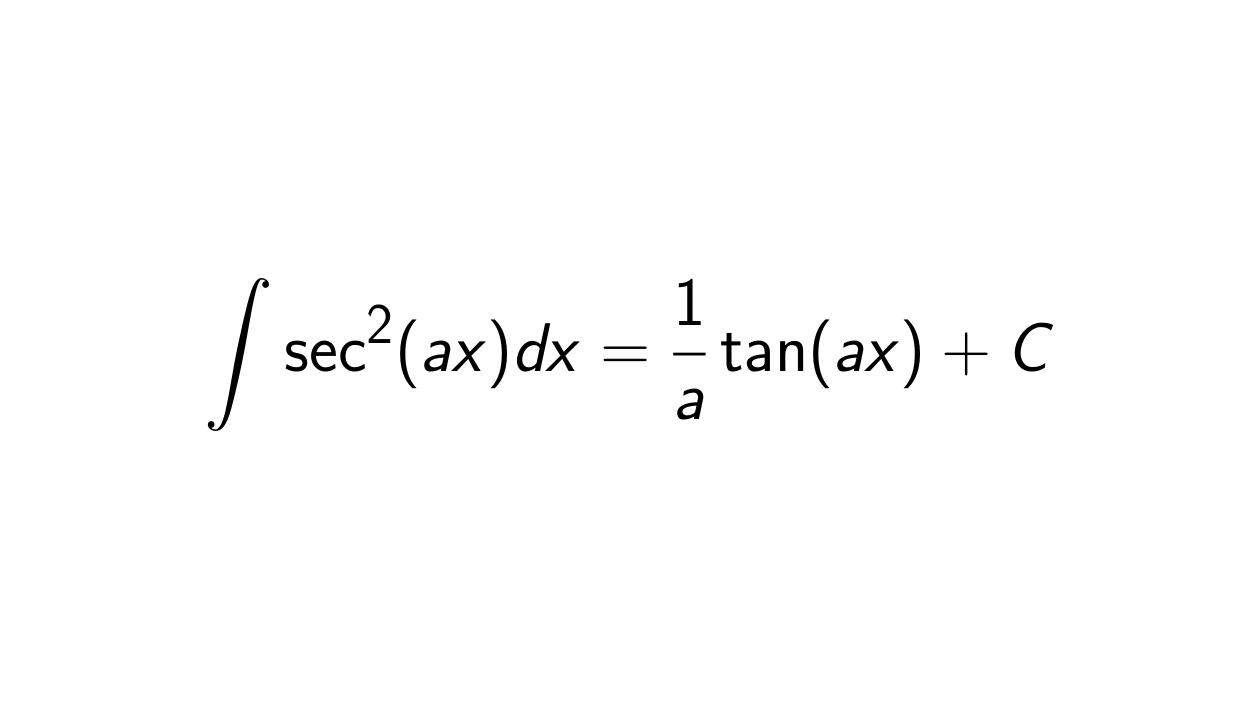The integral of
\sec^2(ax) is
\frac{1}{a}\tan(ax) + C.
Proof. In this case, it is easy to show what the integral
\sec^2(ax) is if you have seen derivatives. Notice that we have seen
here that
\begin{align*}
\frac{d}{dx} \tan(x) = \sec^2(x).
\end{align*}
Taking the antiderivative of
\sec^2(x), we do directly see that:
\begin{align*}
\int \sec^2(x)dx = \tan(x) + C'.
\end{align*}
What about the integral of
\sec^2(ax)? We do know that the derivative of
\frac{1}{a}\tan(ax) is
\sec^2(ax) by using the chain rule. Therefore, taking antiderivative of
\sec^2(ax), we get:
\begin{align*}
\int \sec^2(ax)dx = \frac{1}{a}\tan(ax) + C.
\end{align*}
So, the integral of
\sec^2(ax) is
\frac{1}{a}\tan(ax) + C.