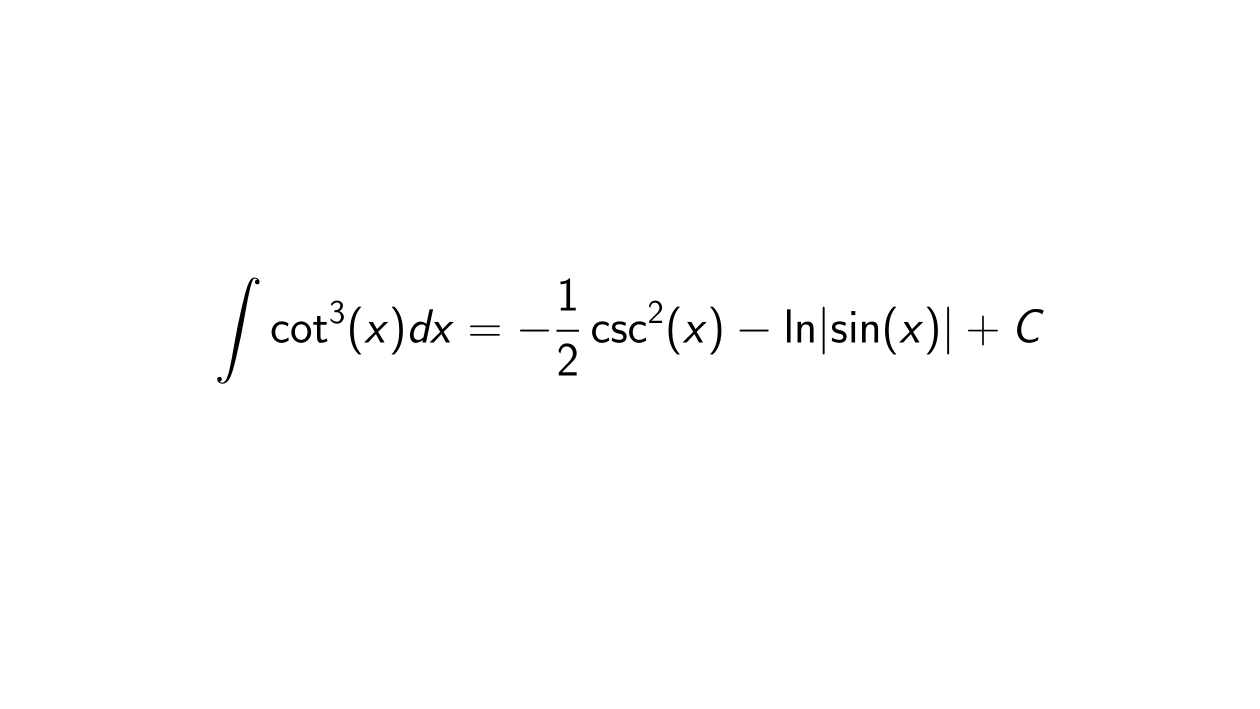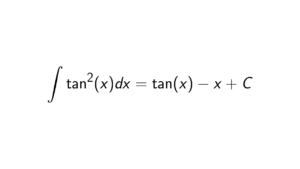What is the integral of cot^3(x)?

integral of cot^3(x)

The integral of

\cot^3(x)

-\frac{1}{2}\csc^2(x) - \ln \lvert \sin(x) \rvert + C

.

Solution. We want to determine the integral of

\cot^3(x)

, which can be simplified by using

\cot^2 = \csc^2(x) - 1

, which we have proven earlier:

\begin{align*} \int \cot^3(x) dx = \int (\csc^2(x) - 1)\cot(x) dx = \int \csc^2(x)\cot(x) dx - \int \cot(x)dx. \end{align*}

We know seen here integral of

\cot(x)

\ln \lvert \sin(x) \rvert

plus some constant. So we have:

\begin{align*} \int \csc^2(x)\cot(x) dx - \int \cot(x)dx = \int \csc^2(x)\cot(x) dx - \ln \lvert \sin(x) \rvert. \end{align*}

We will apply the substitution method. Let

u = \csc(x)

, then

du = -\csc(x)\cot(x)dx

which we have seen here. Then we get the final result everything combined:

\begin{align*} \int \cot^3(x) dx &= \int (\csc^2(x) - 1)\cot(x) dx \\ &= \int \csc^2(x)\cot(x) dx - \int \cot(x)dx \\ &= \int \csc^2(x)\cot(x) dx - \ln \lvert \sin(x) \rvert \\ &= - \int u du - \ln \lvert \sin(x) \rvert \\ &= -\frac{1}{2} u^2 - \ln \lvert \sin(x) \rvert + C \\ &= -\frac{1}{2} \csc^2(x) - \ln \lvert \sin(x) \rvert + C. \end{align*}

Therefore, the integral of

\cot^3(x)

-\frac{1}{2}\csc^2(x) - \ln \lvert \sin(x) \rvert + C