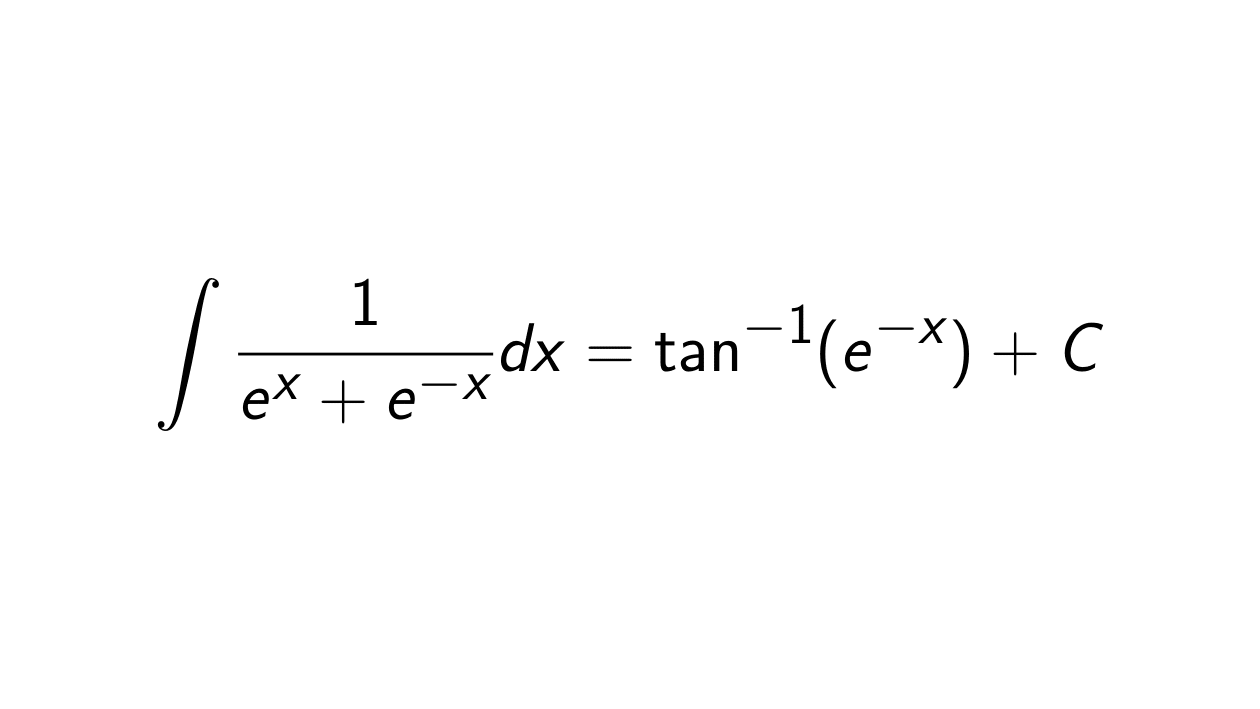What is the integral of 1/(e^x + e^-x)?

integral of 1/(e^x + e^-x)

The integral of

\frac{1}{e^x + e^{-x}}

\tan^{-1}(e^{-x}) + C

.

Solution. We want to determine the integral of

\frac{1}{e^x + e^{-x}}

, i.e.:

\begin{align*} \int \frac{1}{e^x + e^{-x}} dx. \end{align*}

We can rewrite this integral to apply the substitution method later:

\begin{align*} \int \frac{1}{e^x + e^{-x}} dx = \int \frac{1}{e^x(1 + e^{-2x})} dx = \int \frac{e^{-x}}{1 + e^{-2x}} dx. \end{align*}

Let

u = e^{-x}

. We saw here that

du = -e^{-x} dx

. So we get the following:

\begin{align*} \int \frac{e^{-x}}{1 + e^{-2x}} dx &= \int \frac{-du}{1 + u^2} du \\ &= \tan^{-1}(u) + C \\ &= \tan^{-1}(e^{-x}) + C, \end{align*}

where

C

is a constant. Therefore, the integral of

\frac{1}{e^x + e^{-x}}

\tan^{-1}(e^{-x}) + C