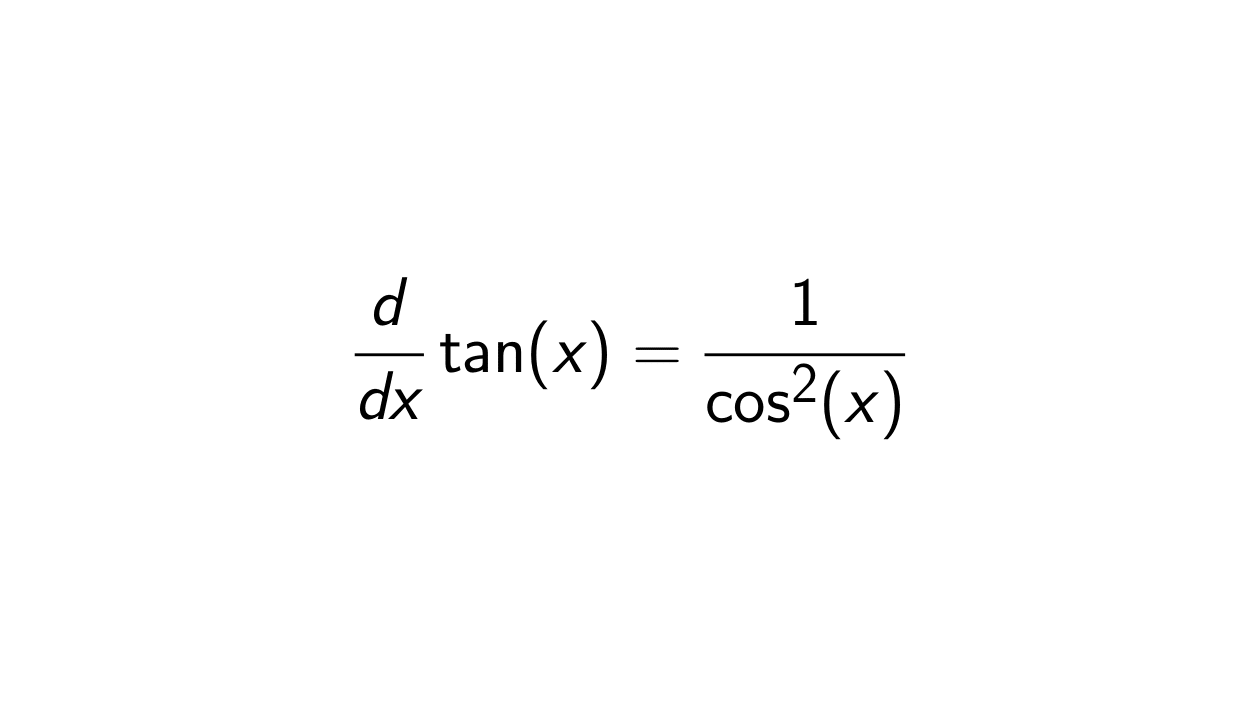What is the Derivative of tan(x)?

derivative of tan(x)

What is the derivative of tan(x)?

We will find out what the derivative of

\tan(x)

is. We will be doing that by the fact that

\tan(x) = \sin(x)/\cos(x)

and apply the quotient rule. We saw earlier a difficult version how to show the derivative of

\tan(x)

with first principle method, but in this article, we take it more easier.

Proof. Let

h(x) = \tan(x) = \frac{\sin(x)}{\cos(x)} = \frac{f(x)}{g(x)}

. Then

\begin{align*} h'(x) = \frac{d}{dx} \bigg(\frac{f(x)}{g(x)}\bigg) = \frac{g(x)f'(x)-f(x)g'(x)}{(g(x))^2}. \end{align*}

We have seen that here that

\frac{d}{dx} \sin(x) = \cos(x)

and here that

\frac{d}{dx} \cos(x) = -\sin(x)

. Therefore, we get

\begin{align*} f'(x) = \cos(x) \quad \text{and} \quad g'(x) = -\sin(x). \end{align*}

Substituting everything together, we get

\begin{align*} h'(x) &= \frac{d}{dx} \bigg(\frac{f(x)}{g(x)}\bigg) \\ &= \frac{g(x)f'(x)-f(x)g'(x)}{(g(x))^2} \\ &= \frac{\cos(x)\cos(x)-\sin(x)(-\sin(x))}{\cos^2(x)} \\ &= \frac{\cos^2(x) + \sin^2(x)}{\cos^2(x)} \\ &= \frac{1}{\cos^2(x)} \\ &= \sec^2(x) \end{align*}

Therefore, we get

h'(x) = \frac{d}{dx} \tan(x) = \frac{1}{\cos^2(x)} = \sec^2(x)