Solution. Let f(x) = \sqrt{x}. Then we can rewrite that as:
\begin{align*}
f(x) = \sqrt{x} = x^{1/2}.
\end{align*}\begin{align*}
f'(x) = \frac{1}{2}x^{-\frac{1}{2}} = \frac{1}{2\sqrt{x}}.
\end{align*}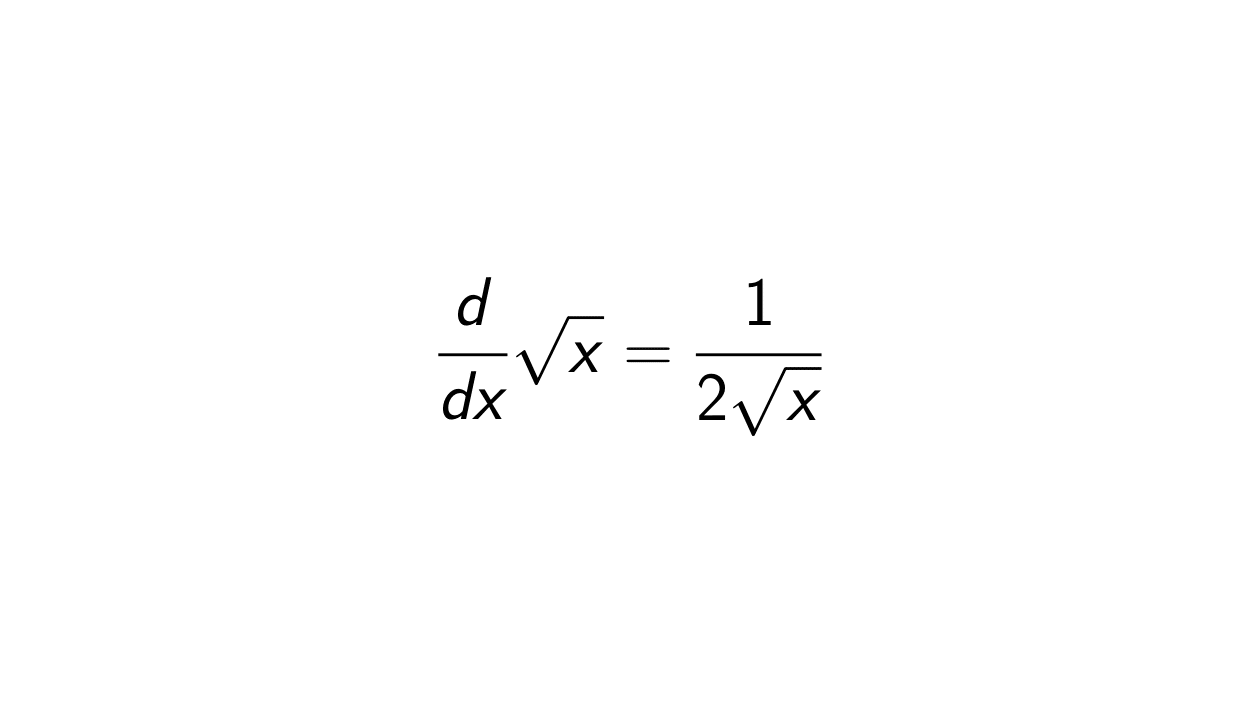
\begin{align*}
f(x) = \sqrt{x} = x^{1/2}.
\end{align*}\begin{align*}
f'(x) = \frac{1}{2}x^{-\frac{1}{2}} = \frac{1}{2\sqrt{x}}.
\end{align*}