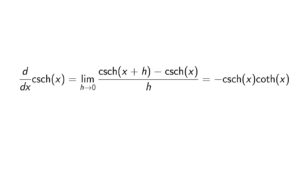
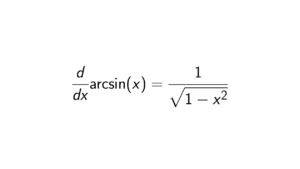What is the Derivative of Hyperbolic Cosine?

derivative of cosh(x)

What is the derivative of Hyperbolic Cosine?

The derivative of

\cosh(x)

\sinh(x)

.

Solution. Let

f(x) = \cosh(x)

. We know by the definition of

\cosh(x)

that

\begin{align*} \cosh(x) = \frac{e^x + e^{-x}}{2}. \end{align*}

Now what is left is to determine the derivative of the exponentials. We have seen here that

\frac{d}{dx} e^x = e^x

and

\frac{d}{dx} e^{-x} = -e^{-x}

. So we get

\begin{align*} f'(x) &= \frac{d}{dx} \cosh(x) \\ &= \frac{d}{dx} \frac{e^x + e^{-x}}{2} \\ &= \frac{d}{dx} \frac{e^x}{2} + \frac{d}{dx} \frac{e^{-x}}{2} \\ &= \frac{e^x}{2} + \frac{-e^{-x}}{2} \\ &= \frac{e^x}{2} - \frac{e^{-x}}{2} \\ &= \frac{e^x - e^{-x}}{2} \\ &= \sinh(x). \end{align*}

In conclusion, we have that the derivative of

\cosh(x)

\sinh(x)