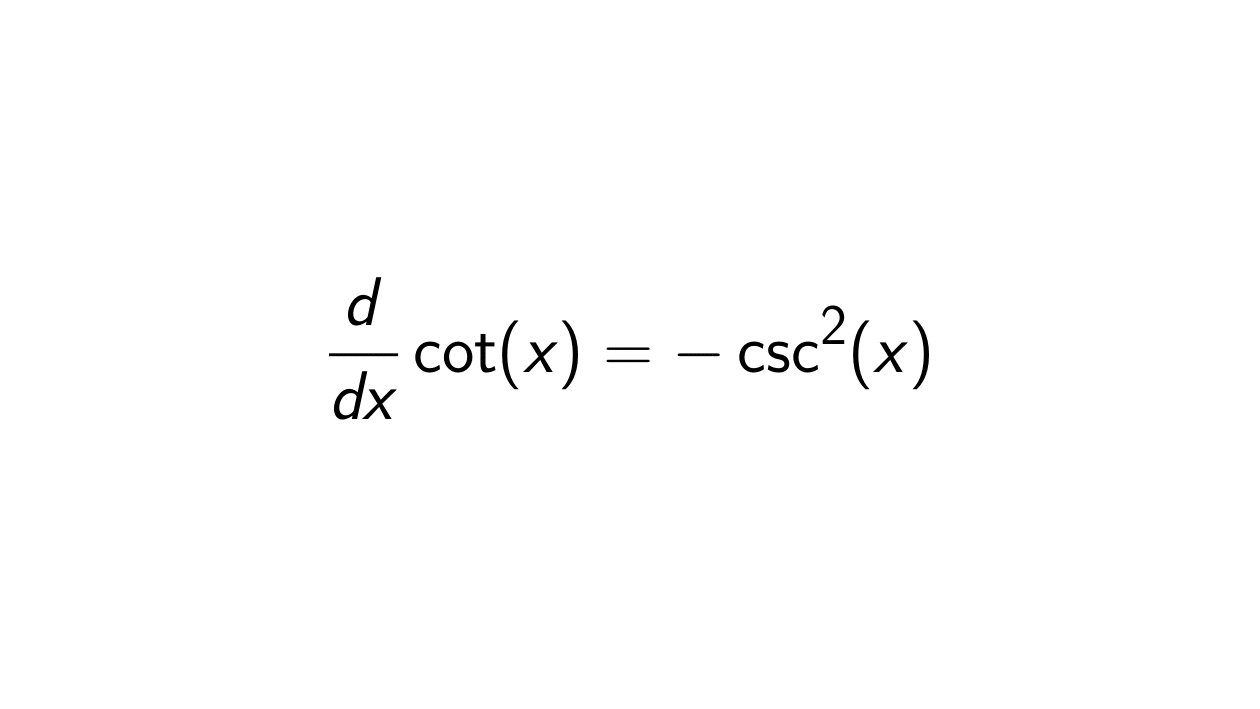Proof. We know that h(x) = \cot(x) = \frac{1}{\tan(x)} = \frac{\cos(x)}{\sin(x)} = \frac{f(x)}{g(x)}. So we will apply the quotient rule:
\begin{align*}
h'(x) = \frac{d}{dx} \bigg(\frac{f(x)}{g(x)}\bigg) = \frac{g(x)f'(x)-f(x)g'(x)}{(g(x))^2}.
\end{align*}\begin{align*}
f'(x) = -\sin(x) \quad \text{and} \quad g'(x) = \cos(x).
\end{align*}\begin{align*}
h'(x) &= \frac{d}{dx} \bigg(\frac{f(x)}{g(x)}\bigg) \\
&= \frac{g(x)f'(x)-f(x)g'(x)}{(g(x))^2} \\
&= \frac{\sin(x)\cdot(-\sin(x)) - \cos(x)\cdot \cos(x)}{\sin^2(x)} \\
&= \frac{-\sin^2(x) - \cos^2(x)}{\sin^2(x)} \\
&= \frac{-1}{\sin^2(x)} \\
&= -\csc^2(x).
\end{align*}