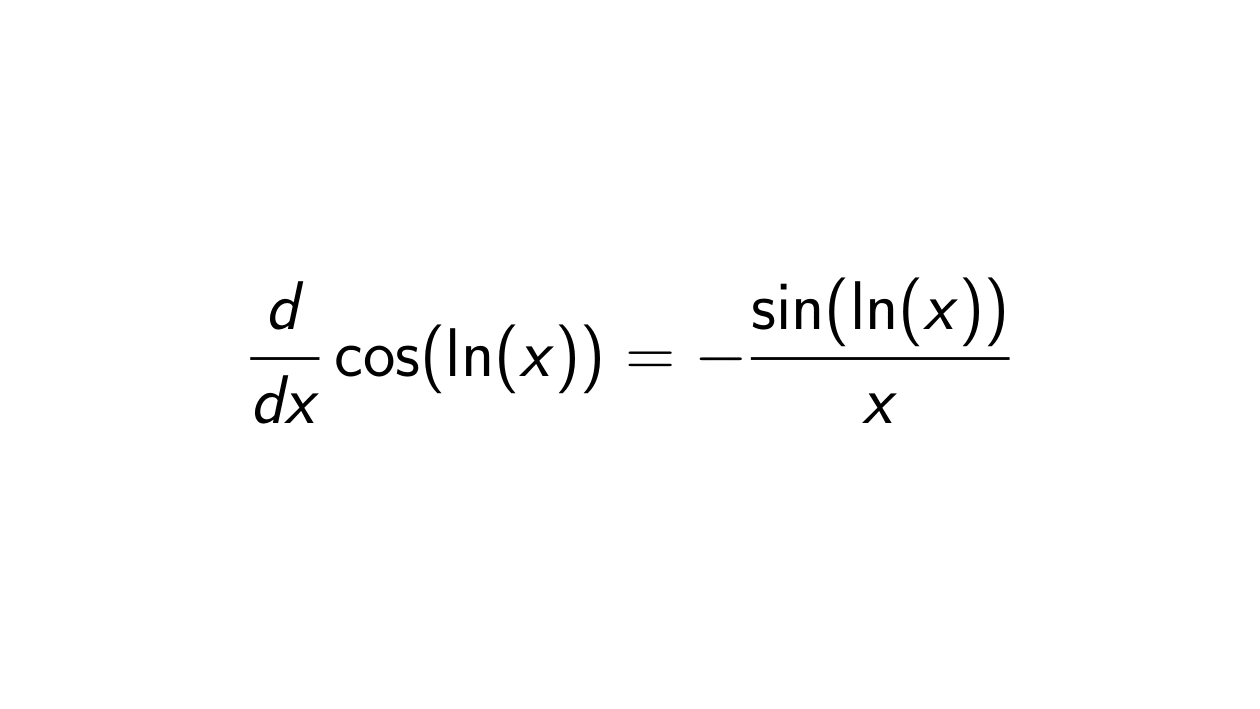Solution. We will use the chain rule to find out what the derivative of F(x) = f(g(x)) = \cos(\ln(x)) is. In other words, we will use the following:
\begin{align*}
F'(x) = f'(g(x))g'(x),
\end{align*}\begin{align*}
f'(g(x)) = -\sin(g(x)) = -\sin(\ln(x)).
\end{align*}\begin{align*}
F'(x) &= f'(g(x))g'(x) \\
&= -\sin(\ln(x))\frac{1}{x} \\
&= -\frac{\sin(\ln(x))}{x}.
\end{align*}