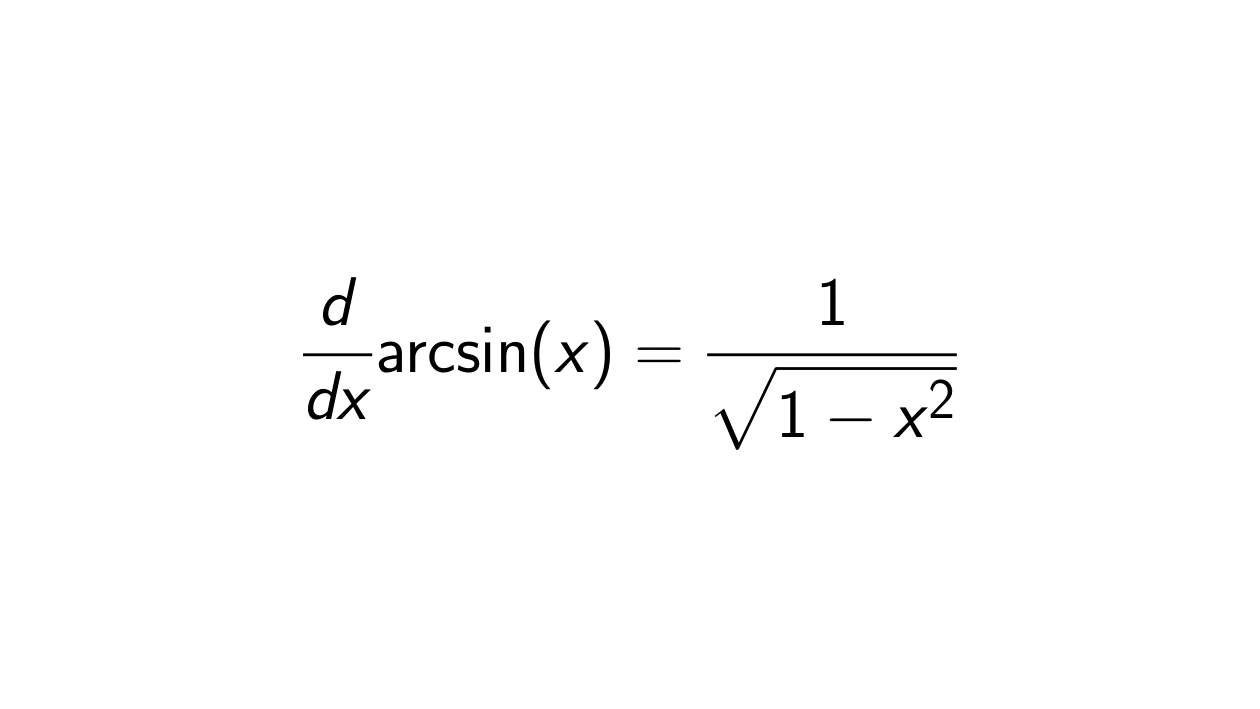What is the Derivative of arcsin(x)?

Derivative of arcsin(x)

The derivative of

\arcsin(x)

\frac{1}{\sqrt{1-x^2}}

.

Solution. Let

y = \sin^{-1}(x)

. Then

x = \sin(y)

and

-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}

. We will differentiate with respect to

x

\begin{align*} \frac{d}{dx} x = \frac{d}{dx} \sin(y) &\iff 1 = \frac{d(sin(y))}{dy} \frac{dy}{dx} \\ &\iff 1 = \cos(y) \frac{dy}{dx} \\ &\iff \frac{dy}{dx} = \frac{1}{\cos(y)}, \end{align*}

where we have seen here that

\frac{d(sin(y))}{dy} = \cos(y)

. We have that

\cos(y) \geq 0

-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}

. Since

\sin^2(y) + \cos^2(y) = 1

, we have that:

\begin{align*} \cos^2(y) = 1 - \sin^2(y) \iff \cos(y) = \sqrt{1 - \sin^2(y)}. \end{align*}

where

\sin^2(y) = x^2

since

\sin(y) = x

. Substituting everything, we get that the derivative of

\arcsin(x)

is:

\begin{align*} \frac{d}{dx} \arcsin(x) = \frac{d}{dx} \sin^{-1}(x) = \frac{dy}{dx} = \frac{1}{\cos(y)} = \frac{1}{\sqrt{1-x^2}}, \quad x \in (-1,1). \end{align*}

So, the derivative of

\arcsin(x)

\frac{1}{\sqrt{1-x^2}}