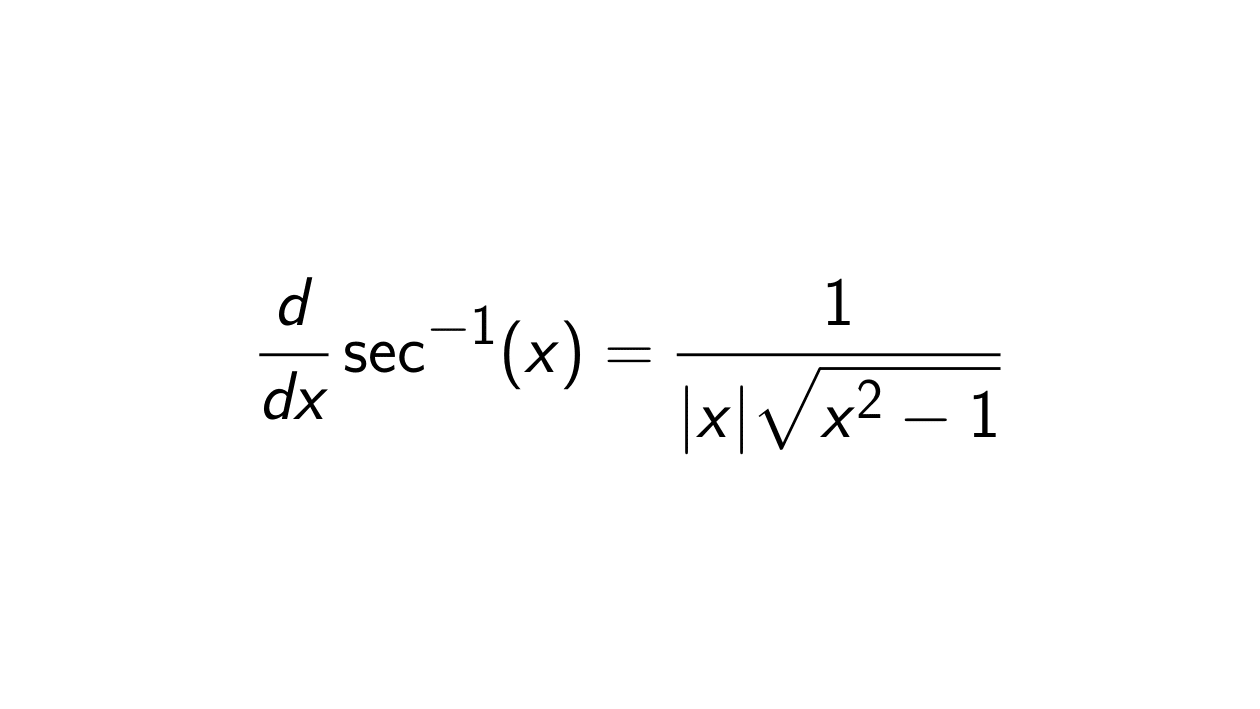Solution. Let F(x) = \sec^{-1}(x) = \text{arcsec}(x) with \lvert x \rvert \geq 1. We have seen here that
\begin{align*}
F(x) = \sec^{-1}(x) = \cos^{-1}(1/x).
\end{align*}\begin{align*}
F'(x) = f'(g(x))g'(x).
\end{align*}\begin{align*}
f'(u) = \frac{d}{du} \cos^{-1}(u) = \frac{-1}{\sqrt{1 - u^2}}
\end{align*}\begin{align*}
g'(x) = -\frac{1}{x^2}.
\end{align*}\begin{align*}
f'(g(x)) = \frac{-1}{\sqrt{1 - g(x)^2}} = \frac{-1}{\sqrt{1 - \frac{1}{x^2}}}.
\end{align*}\begin{align*}
F'(x) &= f'(g(x))g'(x) \\
&= \frac{-1}{\sqrt{1 - \frac{1}{x^2}}} \Bigg(-\frac{1}{x^2}\Bigg) \\
&= \frac{1}{x^2} \frac{1}{\sqrt{1 - \frac{1}{x^2}}} \\
&= \frac{1}{x^2} \frac{1}{\sqrt{\frac{x^2 - 1}{x^2}}} \\
&= \frac{1}{x^2} \frac{\sqrt{x^2}}{\sqrt{x^2 - 1}} \\
&= \frac{1}{x^2} \frac{\lvert x \rvert}{\sqrt{x^2 - 1}} \\
&= \frac{1}{\lvert x \rvert} \frac{1}{\sqrt{x^2 - 1}} \\
&= \frac{1}{\lvert x \rvert \sqrt{x^2 - 1}}.
\end{align*}\begin{align*}
F'(x) = \frac{d}{dx} \text{arcsec}(x) = \frac{d}{dx} \sec^{-1}(x) = \frac{1}{\lvert x \rvert \sqrt{x^2 - 1}}.
\end{align*}