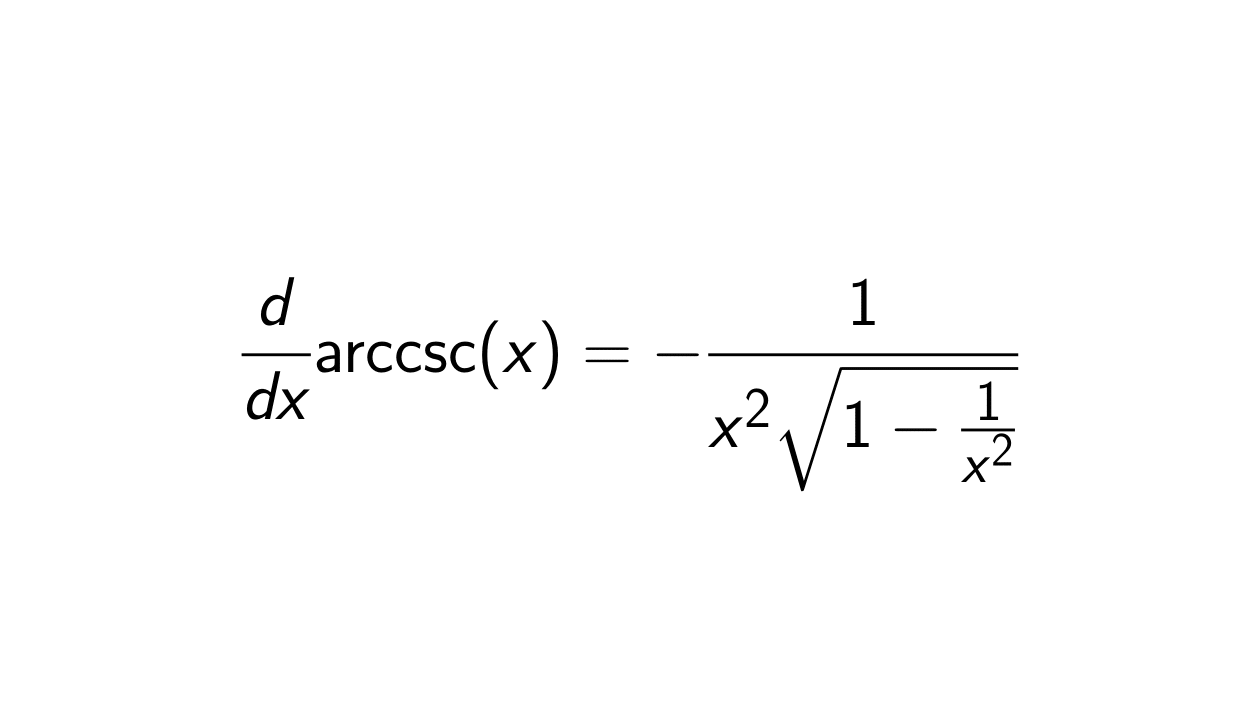What is the Derivative of arccsc(x)?

derivative of arccsc(x)

The derivative of

\text{arccsc}(x)

-\frac{1}{x^2\sqrt{1 - \frac{1}{x^2}}}

.

Solution. Let

F(x) = \csc^{-1}(x)

where

\lvert x \rvert \geq 1

. We have seen here that

\begin{align*} F(x) = \csc^{-1}(x) = \sin^{-1}(1/x), \quad \lvert x \rvert \geq 1. \end{align*}

We need to use the chain rule to determine the derivative of

\sin^{-1}(1/x)

. Let

f(u) = \sin^{-1}(u)

and

g(x) = \frac{1}{x}

such that

F(x) = f(g(x))

. Then

\begin{align*} F'(x) = f'(g(x))g'(x). \end{align*}

We have seen here that

f'(u) = \frac{1}{\sqrt{1 - u^2}}

and here that

g'(x) = \frac{-1}{x^2}

. So we get:

\begin{align*} f'(g(x)) = \frac{1}{\sqrt{1 - g(x)^2}} = \frac{1}{\sqrt{1 - \frac{1}{x^2}}}. \end{align*}

Substituting everything, we get:

\begin{align*} F'(x) &= f'(g(x))g'(x) \\ &= \frac{1}{\sqrt{1 - \frac{1}{x^2}}} \cdot \frac{-1}{x^2} \\ &= \frac{-1}{x^2\sqrt{1 - \frac{1}{x^2}}}. \end{align*}

So, the derivative of

\text{arccsc}(x)

-\frac{1}{x^2\sqrt{1 - \frac{1}{x^2}}}