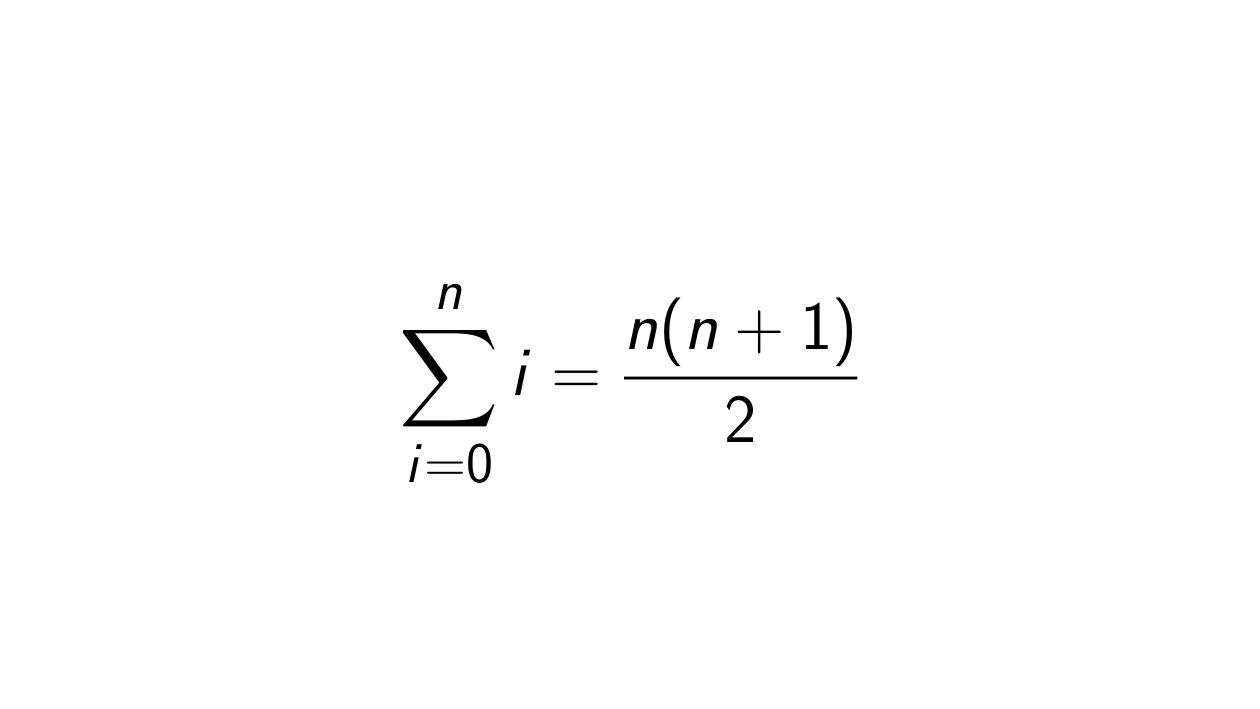Blog

You are currently viewing The Finite Sum Of Natural Numbers
Finite sum of natural numbers

The Finite Sum Of Natural Numbers

In this article, we will prove the finite sum of natural numbers via the direct way and induction. We have the following sum, which is the finite sum of natural numbers
∑i=0ni=n(n+1)2\begin{equation*} \sum_{i = 0}^n i = \frac{n(n+1)}{2} \end{equation*}
Proof 1. We start with induction. For the base case, if n=0n = 0, then
∑i=00i=0=0(0+1)2=0\begin{equation*} \sum_{i = 0}^0 i = 0 = \frac{0(0+1)}{2} = 0 \end{equation*}
which holds. For the induction step, we take for the induction hypothesis that the sum holds for nn, and we want to show that it holds too for n+1n + 1. So summing up to and including n+1n + 1, we get
∑i=0n+1i=(n+1)((n+1)+1)2=n(n+1)+2n+22=n(n+1)2+2n+22=n(n+1)2+(n+1)=(∑i=0ni)+(n+1)=∑i=0n+1i\begin{align*} \sum_{i = 0}^{n+1} i &= \frac{(n + 1)((n + 1) +1)}{2} \\ &= \frac{n(n+1) + 2n + 2}{2} \\ &= \frac{n(n+1)}{2} + \frac{2n + 2}{2} \\ &= \frac{n(n+1)}{2} + (n + 1) \\ &= (\sum_{i = 0}^{n} i) + (n + 1) = \sum_{i = 0}^{n + 1} i \end{align*}
which proves that the summation is correct.

Proof 2. Another way to prove it is to reverse the sum from nn to 00, i.e.,
n+(n−1)+⋯+2+1\begin{align*} n + (n-1) + \cdots + 2 + 1 \end{align*}
Now we take the sum which we have seen earlier and the reverse version:
1+2+⋯+(n−1)+nn+(n−1)+⋯+2+1\begin{alignat*}{4} 1 &+ 2 &&+ \cdots &&+ (n - 1) &&+ n \\ n &+ (n-1) &&+ \cdots &&+ 2 &&+ 1\\ \end{alignat*}
We will sum the two sums above: n+1=n+1n + 1 = n + 1, (n−1)+2=n+1(n - 1) + 2 = n + 1, …\ldots, 1+n=n+11 + n = n + 1. This happens nn times. So we get
2⋅∑i=0ni=n(n+1)\begin{equation*} 2 \cdot \sum_{i = 0}^n i = n(n + 1) \end{equation*}
Now divide out 22 on both sides, and we get
∑i=0ni=n(n+1)2\begin{equation*} \sum_{i = 0}^n i = \frac{n(n+1)}{2} \end{equation*}
which finishes the proof.
Tags: ,

Leave a Reply