Proof. Recall that we have the next addition formula for Sine:
\begin{align*}
\sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B).
\end{align*}\begin{align*}
\sin(x + x) = \sin(x)\cos(x) + \cos(x)\sin(x) &\iff \sin(2x) = 2\sin(x)\cos(x),
\end{align*}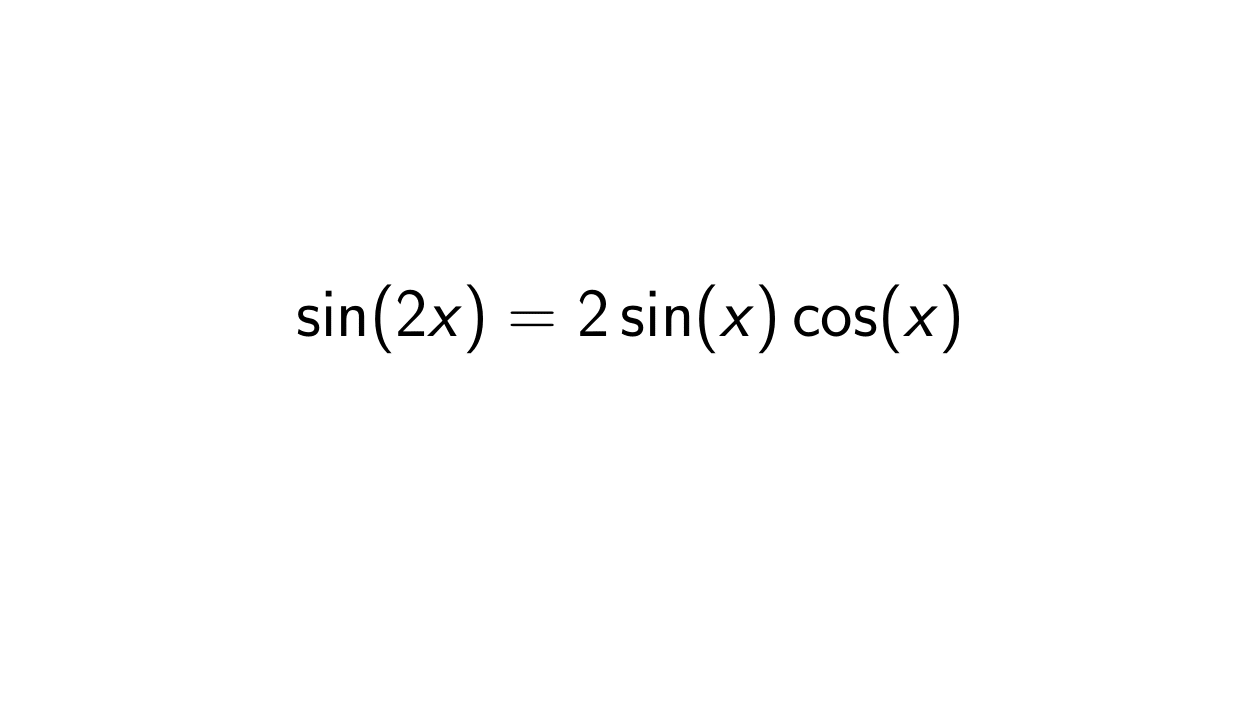
\begin{align*}
\sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B).
\end{align*}\begin{align*}
\sin(x + x) = \sin(x)\cos(x) + \cos(x)\sin(x) &\iff \sin(2x) = 2\sin(x)\cos(x),
\end{align*}