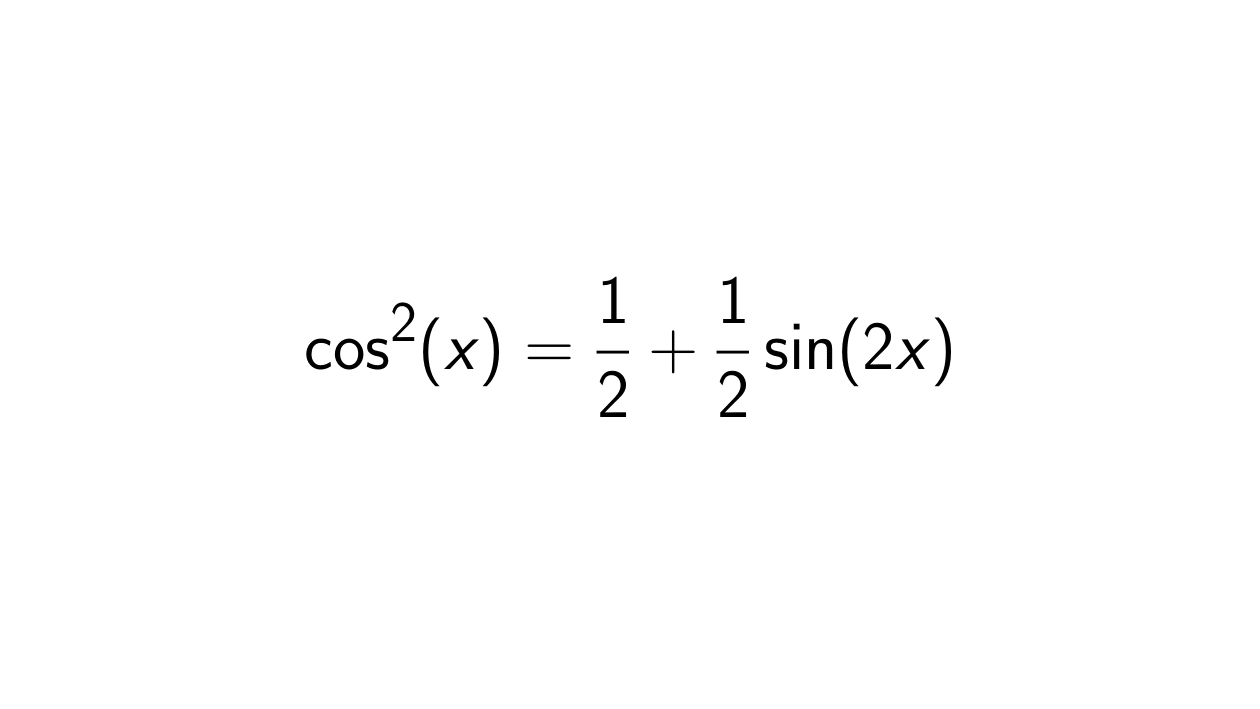Prove that cos^2(x) = 1/2 + 1/2 cos(2x)

Show that

\cos^2(x)

is equal to

\frac{1}{2} + \frac{1}{2}\cos(2x)

.

Proof. We will use the next addition formula for Cosine:

\begin{align*} \cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B). \end{align*}

Let

A = B = x

. Then we get the following:

\begin{align*} \cos(x + x) = \cos(x)\cos(x) - \sin(x)\sin(x) &\iff \cos(2x) = \cos^2(x) - \sin^2(x). \end{align*}

From here we see that

\sin^2(x) = 1 - \cos^2(x)

. So we get:

\begin{align*} \cos(2x) = \cos^2(x) - (1 - \cos^2(x)) &\iff \cos(2x) = 2\cos^2(x) - 1 \\ &\iff \cos^2(x) = \frac{1}{2} + \frac{1}{2}\cos(2x) \end{align*}

Therefore,

\cos^2(x)

is equal to

\frac{1}{2} + \frac{1}{2}\cos(2x)