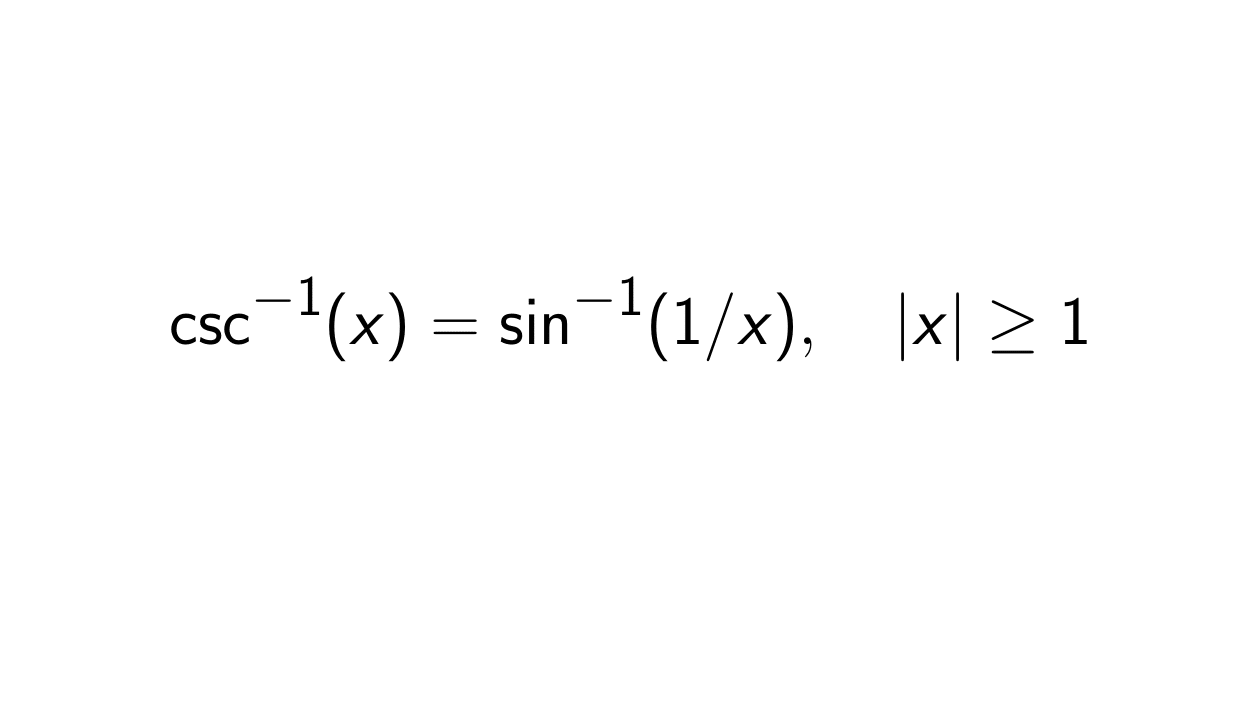Prove that csc^-1(x) = sin^-1(1/x)

arccsc(x) is equal to arcsin(1/x)

We will prove that

\csc^{-1}(x) = \sin^{-1}(1/x)

for

\lvert x \rvert \geq 1

.

Proof. Notice that the functions

\csc^{-1}(x)

and

\sin^{-1}(1/x)

are defined on the next intervals:

\begin{align*} \csc^{-1}(x) \text{ where } \lvert x \rvert \geq 1 \end{align*}

and:

\begin{align*} \sin^{-1}(x) \text{ where } -1 \leq x \leq 1. \end{align*}

Let

y = \csc^{-1}(x)

. Then

\begin{align*} y = \csc^{-1}(x) &\iff \csc(y) = x \\ &\iff \frac{1}{\sin(y)} = x \quad \text{since } \csc(y) = \frac{1}{\sin(y)} \\ &\iff \sin(y) = \frac{1}{x} \\ &\iff y = \sin^{-1}(1/x). \end{align*}

Since

y = \csc^{-1}(x)

, we have that

\csc^{-1}(x) = \sin^{-1}(1/x)

for

-1 \leq 1/x \leq 1

. Inverting the intervals results

\lvert x \rvert \geq 1

for

\csc^{-1}(x) = \sin^{-1}(1/x)