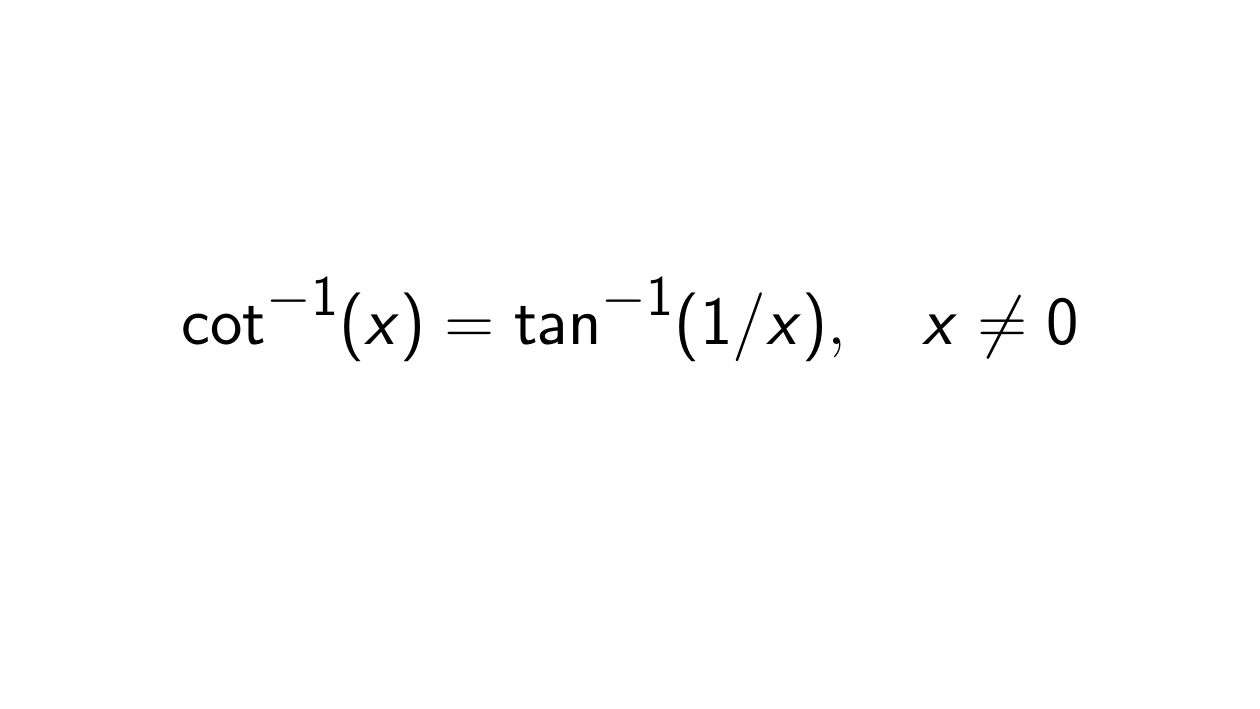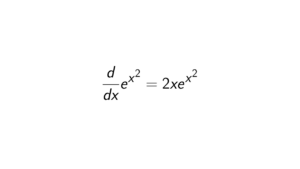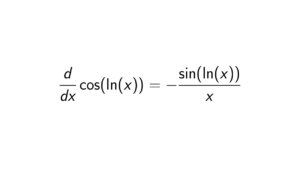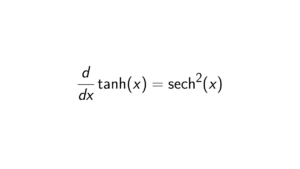Proof. Take the following functions into account:
\begin{align*}
\cot^{-1}(x), \text{ where } x \neq 0,
\end{align*}\begin{align*}
\tan^{-1}(x), \text{ where } x \text{ is defined everywhere.}
\end{align*}\begin{align*}
y = \cot^{-1}(x) &\iff \cot(y) = x \\
&\iff \frac{1}{\tan(y)} = x \\
&\iff y = \tan^{-1}(1/x),
\end{align*}