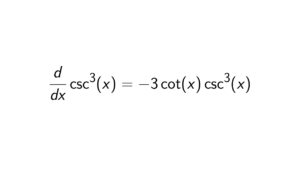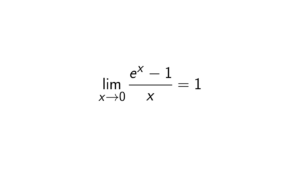How to prove the quotient rule derivative using first principle of derivatives

Proving the quotient rule can be easily done if you know to apply one trick, see the following section.

Proof of quotient rule derivative using first principle of derivatives

Let

f

and

g

be functions that are differentialbe at

x

and

g(x) \neq 0

. Then we want to prove the following formula:

\begin{align*} \bigg(\frac{f}{g}\bigg)'(x) = \frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2}, \end{align*}

with the first principle of derivatives.

\begin{align*} \bigg(\frac{f}{g}\bigg)'(x) &= \lim_{h \rightarrow 0} \frac{\frac{f(x+h)}{g(x+h)} - \frac{f(x)}{g(x)}}{h} \\ &= \lim_{h \rightarrow 0} \frac{f(x+h)g(x) - f(x)g(x+h)}{g(x+h)g(x)h}. \\ \end{align*}

Now the trick we need to apply is

- f(x)g(x) + f(x)g(x) = 0

and we place that in the above numerator:

\begin{align*} & \lim_{h \rightarrow 0} \frac{f(x+h)g(x) - f(x)g(x+h)}{g(x+h)g(x)h} = \\ & \lim_{h \rightarrow 0} \frac{f(x+h)g(x) - f(x)g(x) + f(x)g(x) - f(x)g(x+h)}{g(x+h)g(x)h} = \\ & \lim_{h \rightarrow 0} \frac{g(x)(f(x+h) - f(x)) - f(x)(g(x + h) - g(x))}{g(x+h)g(x)h} = \\ & g(x)\lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{g(x+h)g(x)h} - f(x)\lim_{h \rightarrow 0} \frac{g(x + h) - g(x)}{g(x+h)g(x)h} = \\ & \frac{g(x)f'(x)}{(g(x))^2} - \frac{f(x)g'(x)}{(g(x))^2} = \\ & \frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2}, \end{align*}

where we have now proved the quotient rule.