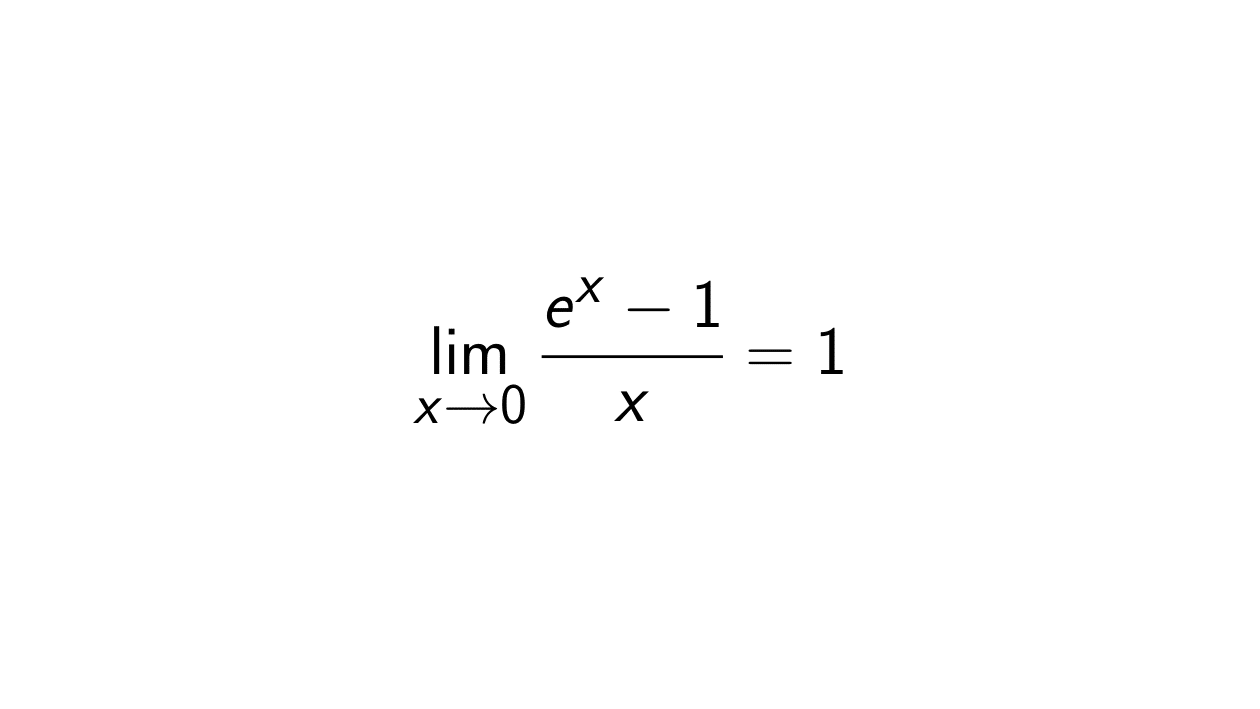Proof. If we apply the Bernoulli inequality and let n \rightarrow \infty, then we get
\begin{align*}
1 + x \leq e^x.
\end{align*}\begin{align*}
1 + x \leq e^x \leq \frac{1}{1-x}
\end{align*}\begin{align*}
1 \leq \frac{e^x - 1}{x} \leq \frac{1}{1-x}
\end{align*}Proof. This proof is more of circular reasoning, but still valuable to see how easy it works for in the future. We want to determine the next limit:
\begin{align*}
\lim_{x \rightarrow 0} \frac{e^x - 1}{x}
\end{align*}\begin{align*}
e^x &= \sum_{n = 0}^{\infty} \frac{x^n}{n!} \\
&= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots
\end{align*}\begin{align*}
e^x - 1 &= \sum_{n = 1}^{\infty} \frac{x^n}{n!} \\
&= x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots
\end{align*}\begin{align*}
\frac{e^x - 1}{x} &= \sum_{n = 1}^{\infty} \frac{x^{n-1}}{n!} \\
&= 1 + \frac{x}{2!} + \frac{x^2}{3!} + \cdots
\end{align*}\begin{align*}
\lim_{x \rightarrow 0} \frac{e^x - 1}{x} &= \lim_{x \rightarrow 0} \sum_{n = 1}^{\infty} \frac{x^{n-1}}{n!} \\
&= \lim_{x \rightarrow 0} (1 + \frac{x}{2!} + \frac{x^2}{3!} + \cdots) \\
&= 1 + \lim_{x \rightarrow 0} (\frac{x}{2!} + \frac{x^2}{3!} + \cdots) \\
&= 1 + 0 + 0 + 0 + \cdots \\
&= 1.
\end{align*}\begin{align*}
\lim_{x \rightarrow 0} \frac{e^x - 1}{x} = 1
\end{align*}