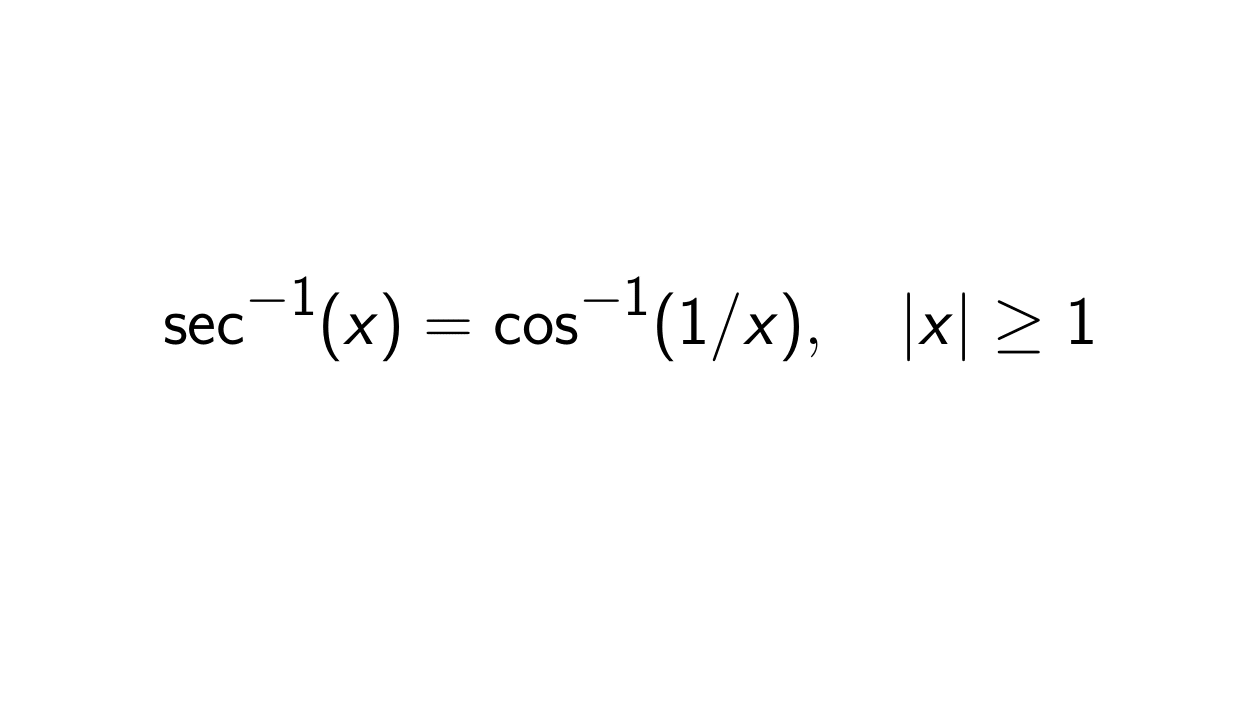Proof. We need to take two things into account:
\begin{align*}
\cos^{-1}(x), \quad -1 \leq x \leq 1,
\end{align*}\begin{align*}
\sec^{-1}(x), \quad \lvert x \rvert \geq 1.
\end{align*}\begin{align*}
y = \sec^{-1}(x) &\iff \sec(y) = x \\
&\iff \frac{1}{\cos(y)} = x \quad \text{since } \sec(y) = \frac{1}{\cos(y)} \\
&\iff \cos(y) = \frac{1}{x} \\
&\iff y = \cos^{-1}(1/x).
\end{align*}