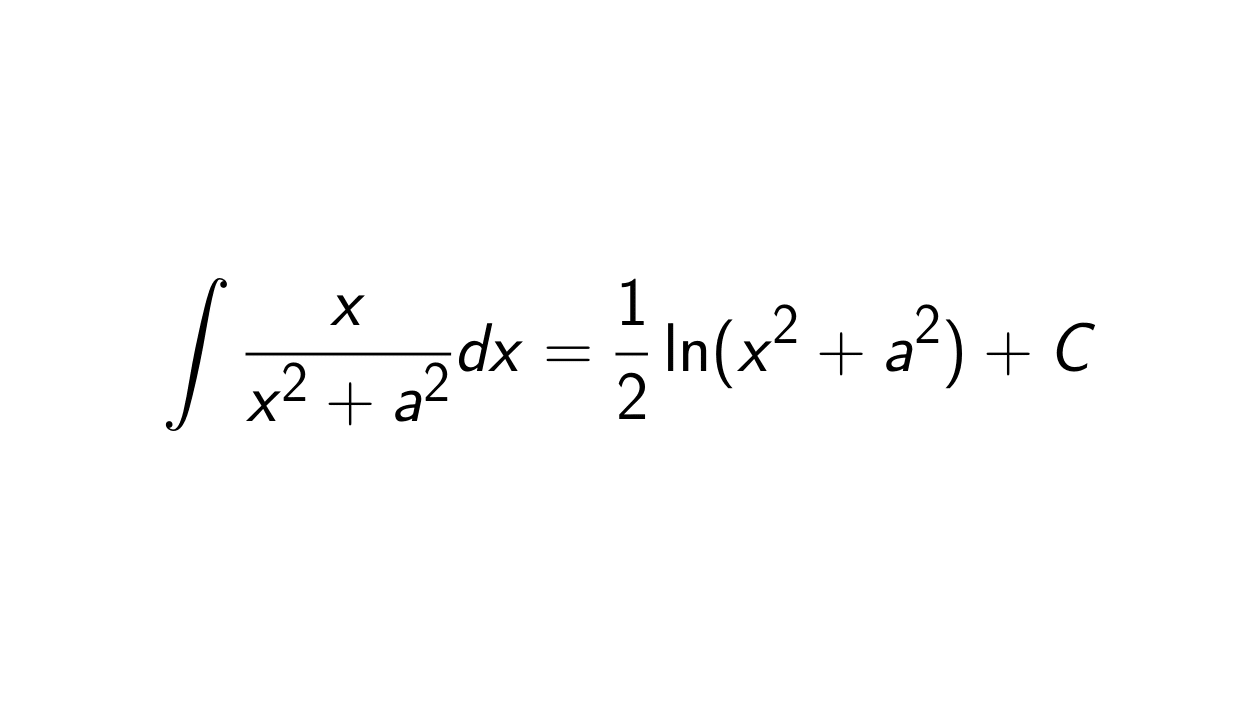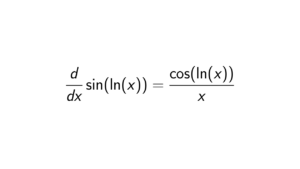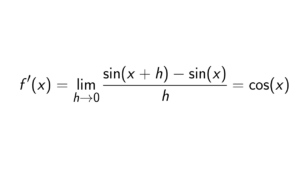What is the integral of x/(x^2 + a^2)?
The integral of
\frac{x}{x^2 + a^2} is
\frac{1}{2}\ln(x^2 + a^2) + C.
Solution of the integral of x/(x^2 + a^2)
We want to determine the integral of
\frac{x}{x^2 + a^2}, i.e.,
\begin{align*}
\int \frac{x}{x^2 + a^2} dx.
\end{align*}
We will use the substitution method. Let
u = x^2 + a^2. Then
du = 2xdx \iff \frac{1}{2}du = xdx. So we get the following integral:
\begin{align*}
\int \frac{x}{x^2 + a^2} dx &= \int \frac{\frac{1}{2}du}{u} \\
&= \frac{1}{2} \int \frac{du}{u} \\
&= \frac{1}{2}\ln \lvert u \rvert + C \\
&= \frac{1}{2}\ln (x^2 + a^2) + C.
\end{align*}Conclusion
So, the integral of
\frac{x}{x^2 + a^2} is
\frac{1}{2}\ln(x^2 + a^2) + C.