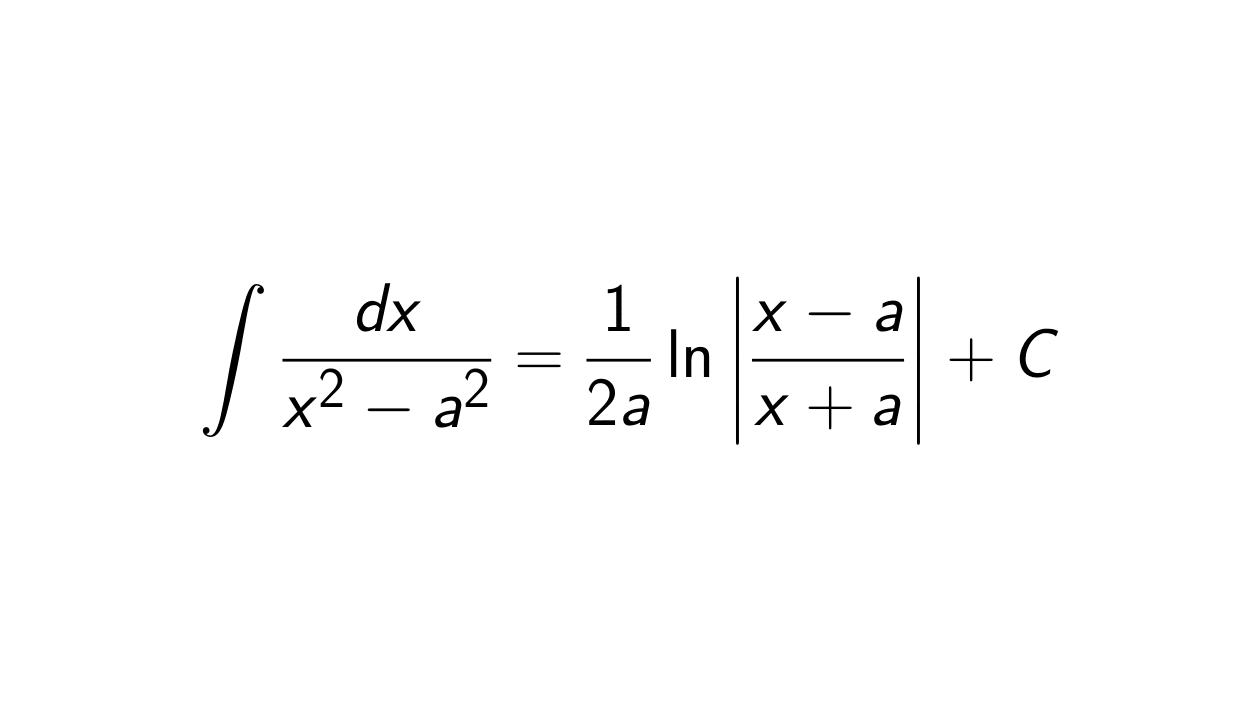What is the integral of 1/(x^2 – a^2)?

The integral of

\frac{1}{x^2 - a^2}

\frac{1}{2a}\ln\lvert \frac{x - a}{x + a} \rvert + C

Solution of the integral 1/(x^2 – a^2)

Solution: We want to determine the next integral:

\begin{align*} \int \frac{dx}{x^2 - a^2}. \end{align*}

We will apply an integral technique such that the denominators will be linear functions:

\begin{align*} \frac{1}{x^2 - a^2} &= \frac{1}{(x-a)(x+a)} \\ &= \frac{A}{x - a} + \frac{B}{x + a} \\ &= \frac{Ax + Aa + Bx - Ba}{x^2 - a^2}. \end{align*}

We do have the following set of equalities:

\begin{align*} A + B &= 0 \\ Aa - Ba &= 1. \end{align*}

We see that

A = -B,

and therefore

B = -\frac{1}{2a}

and

A = \frac{1}{2a}

. Substituting everything above, we get:

\begin{align*} \int \frac{1}{x^2 - a^2} dx &= \int \frac{A}{x - a} dx + \int \frac{B}{x + a} dx \\ &= \frac{1}{2a} \int \frac{dx}{x - a} - \frac{1}{2a} \int \frac{dx}{x + a} \\ &= \frac{1}{2a} \ln \lvert x - a \rvert - \frac{1}{2a} \ln \lvert x + a \rvert + C \\ &= \frac{1}{2a} \ln \bigg\lvert \frac{x - a}{x + a} \bigg\rvert + C. \end{align*}

In conclusion, the integral of

\frac{1}{x^2 - a^2}

\frac{1}{2a}\ln \lvert \frac{x - a}{x + a} \rvert + C

, or in mathematical notation:

\begin{equation*} \int \frac{dx}{x^2 - a^2} = \frac{1}{2a} \ln \bigg\lvert \frac{x - a}{x + a} \bigg\rvert + C. \end{equation*}