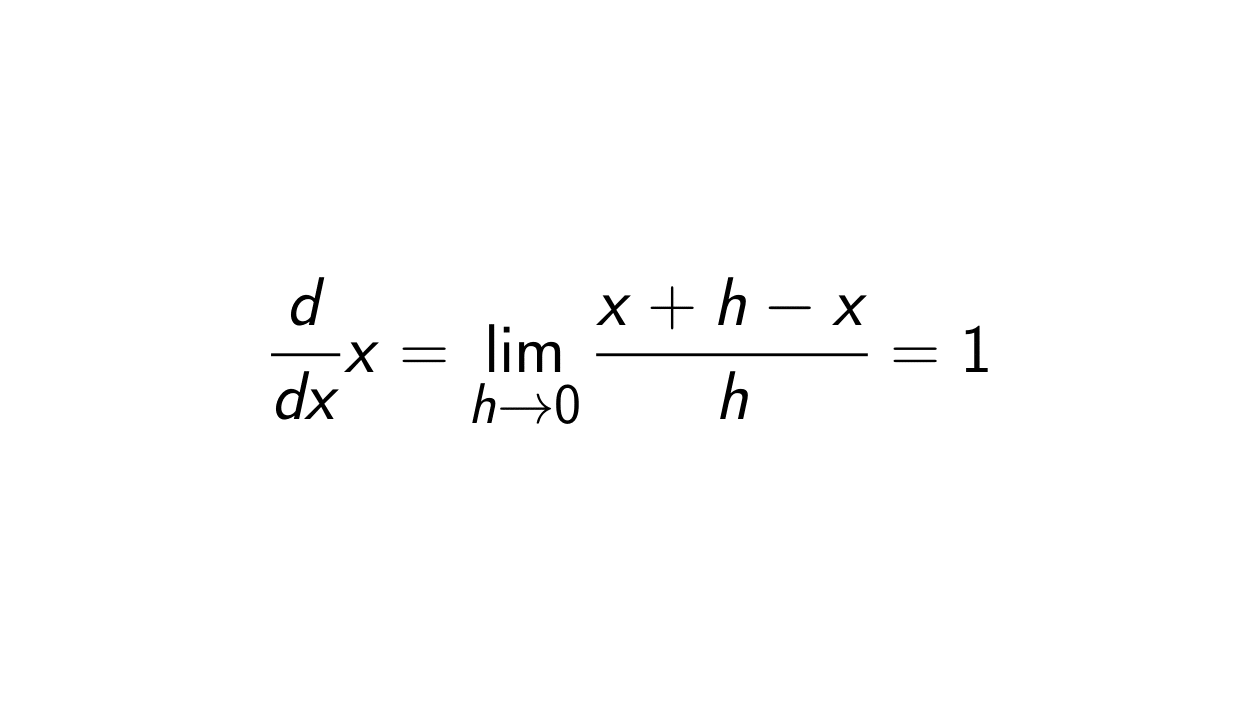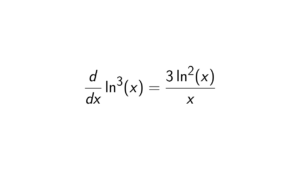Derivative of x using First Principle of Derivatives

The derivative of

x

using the first principle of derivative is 1.

Proof. Let

f(x) = x

. Then we will use the definition of a derivative:

\begin{align*} f'(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{x + h - x}{h} \\ &= \lim_{h \rightarrow 0} \frac{h}{h} \\ &= \lim_{h \rightarrow 0} 1 \\ &= 1. \end{align*}

Therefore, we see that the derivative of

x

is constant, namely, equal to one:

\begin{align*} f'(x) = 1. \end{align*}