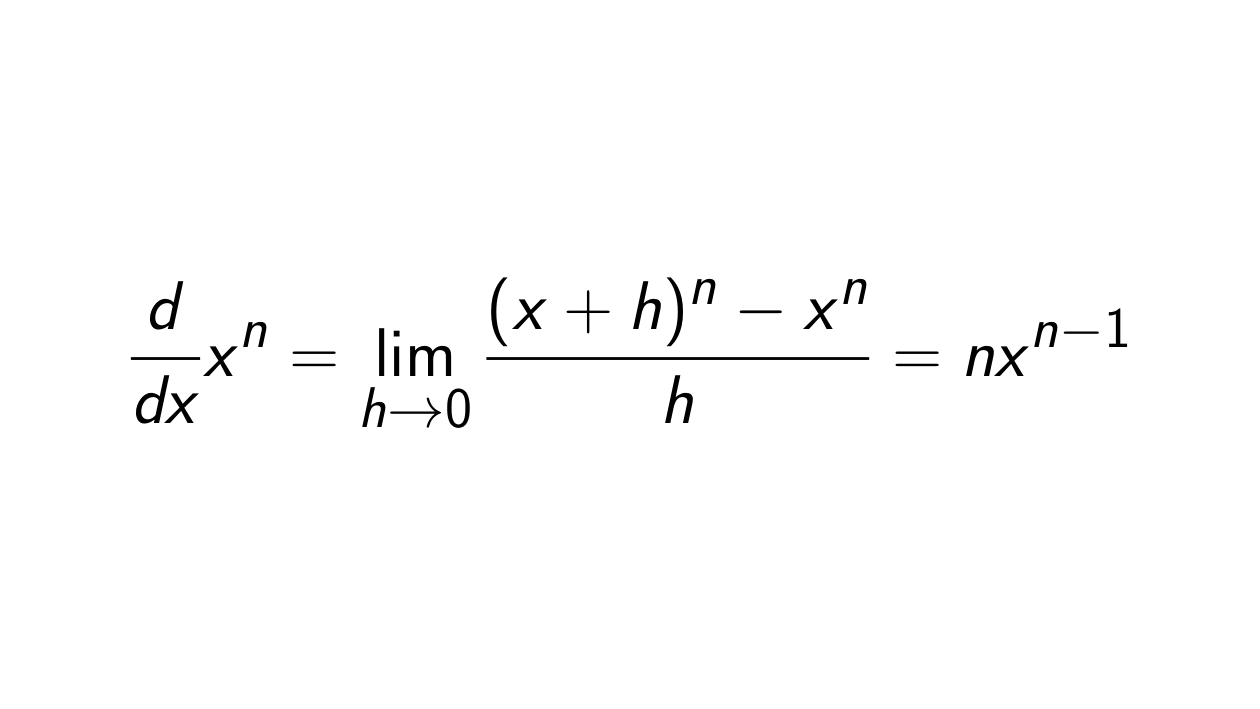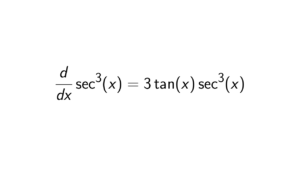Derivative of x^n using First Principle of Derivatives

The derivative of

x^n

nx^{n-1}

using first principle of derivatives.

Proof. Let

f(x) = x^n

. Then using the first principle of derivatives, we get:

\begin{align*} f'(x) &= \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{(x + h)^n - x^n}{h}. \end{align*}

To simplify

(x + h)^n - x^n

, we can use the next identity:

\begin{align*} a^n - b^n = (a-b)(a^{n-1} + a^{n-2}b + a^{n-3}b^2 + \cdots + ab^{n-2} + b^{n-1}), \end{align*}

by letting

a = x + h

and

b = x

. As we see, we have

n

terms in the identity. So we get:

\begin{align*} f'(x) &= \lim_{h \rightarrow 0} \frac{(x + h)^n - x^n}{h} \\ &= \lim_{h \rightarrow 0} \frac{h[(x+h)^{n-1} + (x+h)^{n-2}x + \cdots + (x+h)x^{n-2} + x^{n-1}]}{h} \\ &= \lim_{h \rightarrow 0} ((x+h)^{n-1} + (x+h)^{n-2}x + \cdots + (x+h)x^{n-2} + x^{n-1}) \\ &= (x+0)^{n-1} + (x+0)^{n-2}x + \cdots + (x+0)x^{n-2} + x^{n-1} \\ &= x^{n-1} + x^{n-2}x + \cdots + xx^{n-2} + x^{n-1} \\ &= x^{n-1} + x^{n-1} + \cdots + x^{n-1} + x^{n-1} \\ &= nx^{n-1}. \end{align*}

So, the derivative of

x^n

nx^{n-1}

using first principle of derivatives.