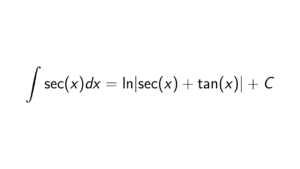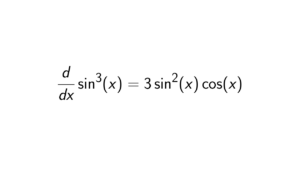Blog

You are currently viewing Derivative of Hyperbolic Cosine using First Principle of Derivatives
Derivative of cosh(x) using First principle of Derivatives

Derivative of Hyperbolic Cosine using First Principle of Derivatives

In this article, we will find the derivative of cosh⁡(x)\cosh(x) using the first principle of derivatives.

Proof. Let f(x)=cosh⁡(x)f(x) = \cosh(x). We know that cosh⁡(x)\cosh(x) is equal to:
cosh⁡(x)=ex+e−x2.\begin{align*} \cosh(x) = \frac{e^x + e^{-x}}{2}. \end{align*}
We want to determine the next limit:
f′(x)=lim⁡h→0f(x+h)−f(x)h=lim⁡h→0cosh⁡(x+h)−cosh⁡(x)h=lim⁡h→0ex+h+e−x−h2−ex+e−x2h=lim⁡h→0ex+h+e−x−h−ex−e−x2h=lim⁡h→0ex(eh−1)+e−x(e−h−1)2h=12exlim⁡h→0eh−1h+12e−xlim⁡h→0e−h−1h\begin{align*} f'(x) &= \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\cosh(x + h) - \cosh(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{e^{x + h} + e^{-x-h}}{2} - \frac{e^x + e^{-x}}{2}}{h} \\ &= \lim_{h \rightarrow 0} \frac{e^{x + h} + e^{-x-h} - e^x - e^{-x}}{2h} \\ &= \lim_{h \rightarrow 0} \frac{e^{x}(e^{h} - 1) + e^{-x}(e^{-h} - 1)}{2h} \\ &= \frac{1}{2}e^x\lim_{h \rightarrow 0} \frac{e^{h} - 1}{h} + \frac{1}{2}e^{-x}\lim_{h \rightarrow 0} \frac{e^{-h} - 1}{h} \end{align*}
Now we do know that from article that lim⁡h→0eh−1h=1\lim_{h \rightarrow 0} \frac{e^{h} - 1}{h} = 1. The lim⁡h→0e−h−1h\lim_{h \rightarrow 0} \frac{e^{-h} - 1}{h} is a little twist from the previous one, where we could substitute −h-h in the Maclaurin series. See the mentioned article. Therefore, we get
12exlim⁡h→0eh−1h+12e−xlim⁡h→0e−h−1h=12(ex−e−x)=sinh⁡(x).\begin{align*} \frac{1}{2}e^x\lim_{h \rightarrow 0} \frac{e^{h} - 1}{h} + \frac{1}{2}e^{-x}\lim_{h \rightarrow 0} \frac{e^{-h} - 1}{h} = \frac{1}{2}(e^x - e^{-x}) = \sinh(x). \end{align*}
Therefore, as conclusion, we have f′(x)=sinh⁡(x)f'(x) = \sinh(x).
Tags: ,

Leave a Reply