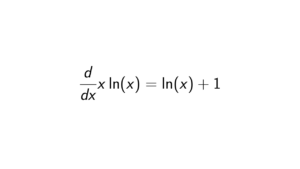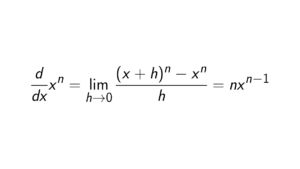Proof. Let f(x) = \csc(x) = \frac{1}{\sin(x)}. Then
\begin{align*}
f'(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\
&= \lim_{h \rightarrow 0} \frac{\csc(x + h) - \csc(x)}{h} \\
&= \lim_{h \rightarrow 0} \frac{\frac{1}{\sin(x + h)} - \frac{1}{\sin(x)}}{h} \\
&= \lim_{h \rightarrow 0} \frac{\frac{\sin(x) - \sin(x + h)}{\sin(x + h)\sin(x)}}{h}
\end{align*}\begin{align*}
\sin(A) - \sin(B) = 2\cos(\frac{A + B}{2})\sin(\frac{A - B}{2}).
\end{align*}\begin{align*}
\sin(x) - \sin(x + h) = 2\cos(\frac{2x + h}{2})\sin(\frac{-h}{2}).
\end{align*}\begin{align*}
\lim_{h \rightarrow 0} \frac{\frac{2\cos(\frac{2x + h}{2})\sin(\frac{-h}{2})}{\sin(x + h)\sin(x)}}{h} &= \lim_{h \rightarrow 0} \frac{\sin(-h/2)}{h/2} \cdot \lim_{h \rightarrow 0} \frac{\cos(\frac{2x + h}{2})}{\sin(x + h)\sin(x)} \\
&= -1 \cdot \lim_{h \rightarrow 0} \frac{\cos(\frac{2x + h}{2})}{\sin(x + h)\sin(x)} \\
&= -1 \cdot \frac{\cos(x)}{\sin^2(x)} \\
&= - \frac{1}{\sin(x)\tan(x)} \\
&= - \csc(x)\cot(x)
\end{align*}