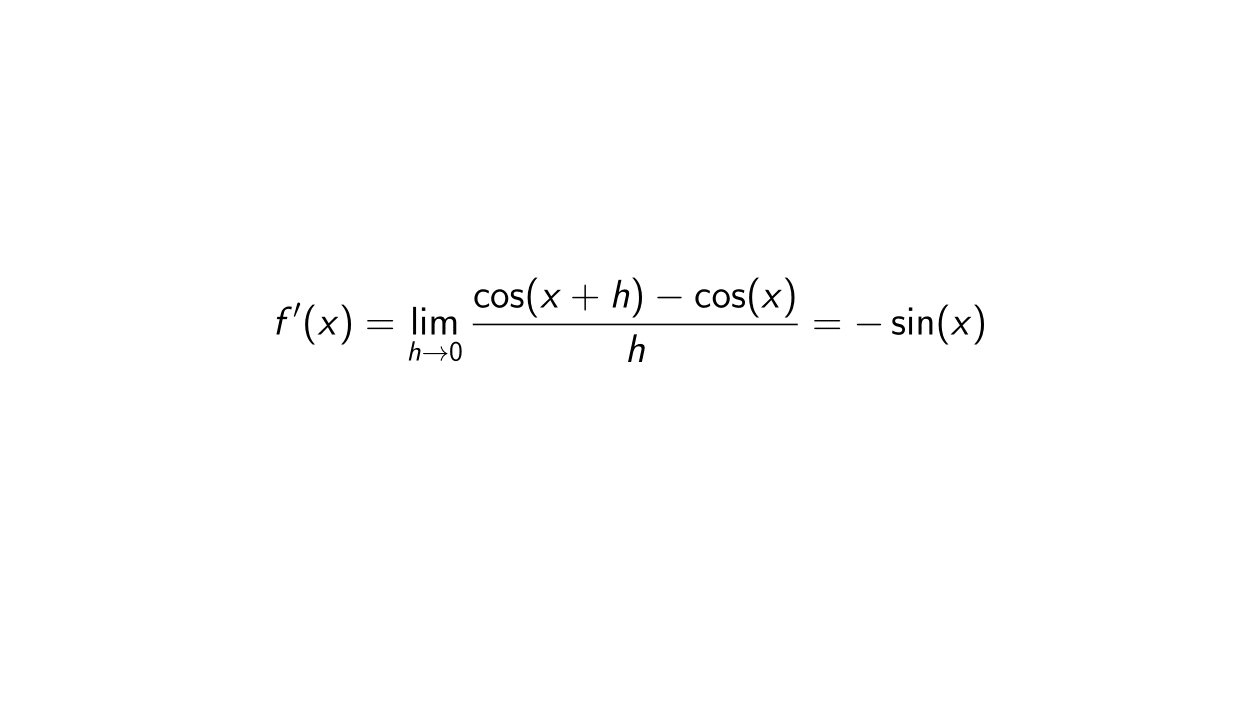Derivative of cos(x) using First Principle of Derivatives

In this article, we will prove the derivative of cosine, or in other words, the derivative of

\cos(x)

, using the first principle of derivatives. We know that the derivative of

\cos(x)

-\sin(x)

, but we would also like to see how to prove that by the definition of the derivative.

Proof. Let

f(x) = \cos(x)

. Then

\begin{align*} f'(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\cos(x + h) - \cos(x)}{h} \end{align*}

Contrary with showing derivative of sin x, we will use a different identity. The reason is that if we apply

\begin{equation*} \cos(x + y) = \cos(x)\cos(y) - \sin(x)\sin(y) \end{equation*}

then we get one limit which goes to infinity (test this out yourself). Therefore, we will use the sum and product formula:

\begin{equation*} \cos(x) - \cos(y) = -2\sin(\frac{x + y}{2})\sin(\frac{x - y}{2}) \end{equation*}

We will apply that identity

\cos(x + h) - \cos(h) = -2\sin(\frac{2x + h}{2})\sin(\frac{h}{2})

and we see that

\begin{align*} \lim_{h \rightarrow 0} \frac{-2\sin(\frac{2x + h}{2})\sin(\frac{h}{2})}{2} &= \lim_{h \rightarrow 0} -\sin(\frac{2x + h}{2}) \lim_{h \rightarrow 0} \frac{2\sin(\frac{h}{2})}{h} \\ &= \lim_{h \rightarrow 0} -\sin(\frac{2x + h}{2}) \lim_{h \rightarrow 0} \frac{\sin(\frac{h}{2})}{h/2} \end{align*}

We know from this article that

\lim_{h \rightarrow 0}\frac{\sin(h)}{h} = 1

. So we get

\begin{align*} \lim_{h \rightarrow 0} -\sin(\frac{2x + h}{2}) = -\sin(2x/2) = -\sin(x). \end{align*}

So we get

f'(x) = -\sin(x)