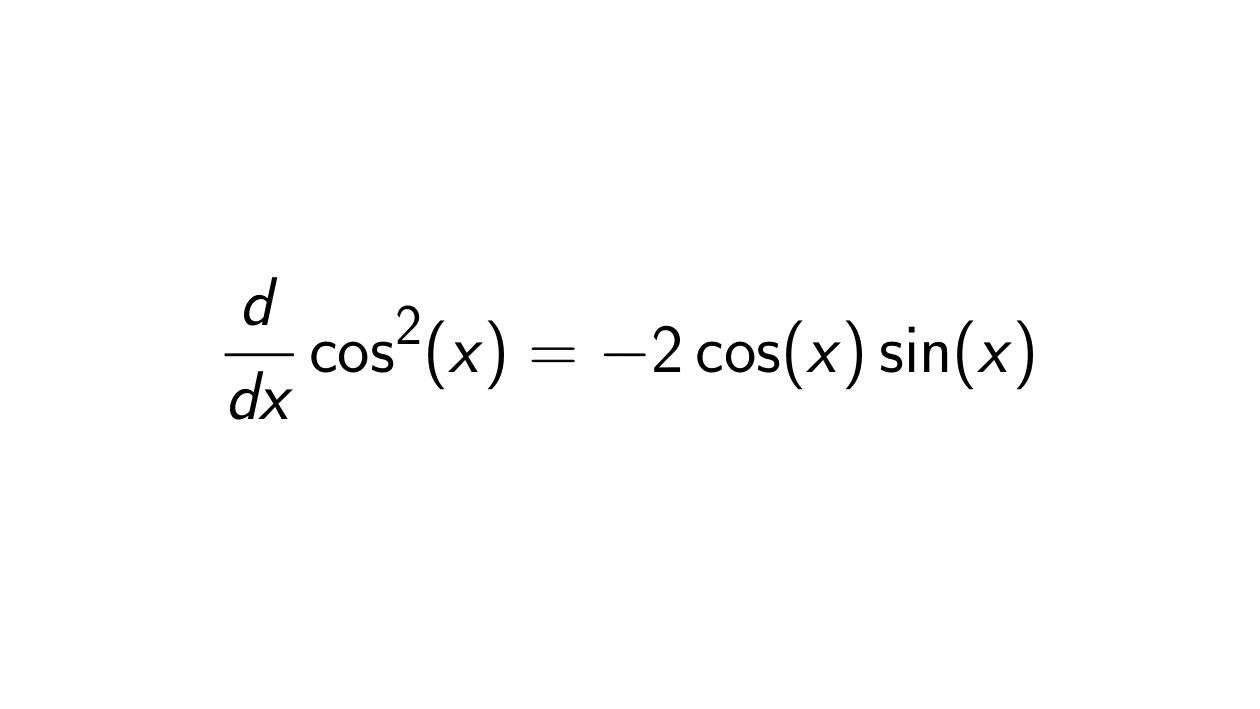Proof 1. Let F(x) = \cos^2(x), f(u) = u^2 and g(x) = \cos(x) such that F(x) = f(g(x)). We will use the chain rule:
\begin{align*}
F'(x) = f'(g(x))g'(x).
\end{align*}\begin{align*}
f'(g(x)) = 2g(x) = 2\cos(x) \quad \text{and} \quad g'(x) = -\sin(x).
\end{align*}\begin{align*}
F'(x) = f'(g(x))g'(x) = -2\cos(x)\sin(x).
\end{align*}\begin{align*}
f'(x) = 2\cos(x)\sin(x).
\end{align*}\begin{align*}
\cos^2(x) = \cos(x)\cos(x)
\end{align*}\begin{align*}
(\cos(x)\cos(x))' = (\cos(x))'\cos(x) + \cos(x)(\cos(x))'
\end{align*}\begin{align*}
(\cos(x))'\cos(x) + \cos(x)(\cos(x))' = -\sin(x)\cos(x) - \cos(x)\sin(x).
\end{align*}\begin{align*}
f'(x) &= (\cos(x)\cos(x))' \\
&= (\cos(x))'\cos(x) + \cos(x)(\cos(x))' \\
&= -\sin(x)\cos(x) - \cos(x)\sin(x) \\
&= -2\cos(x)\sin(x).
\end{align*}