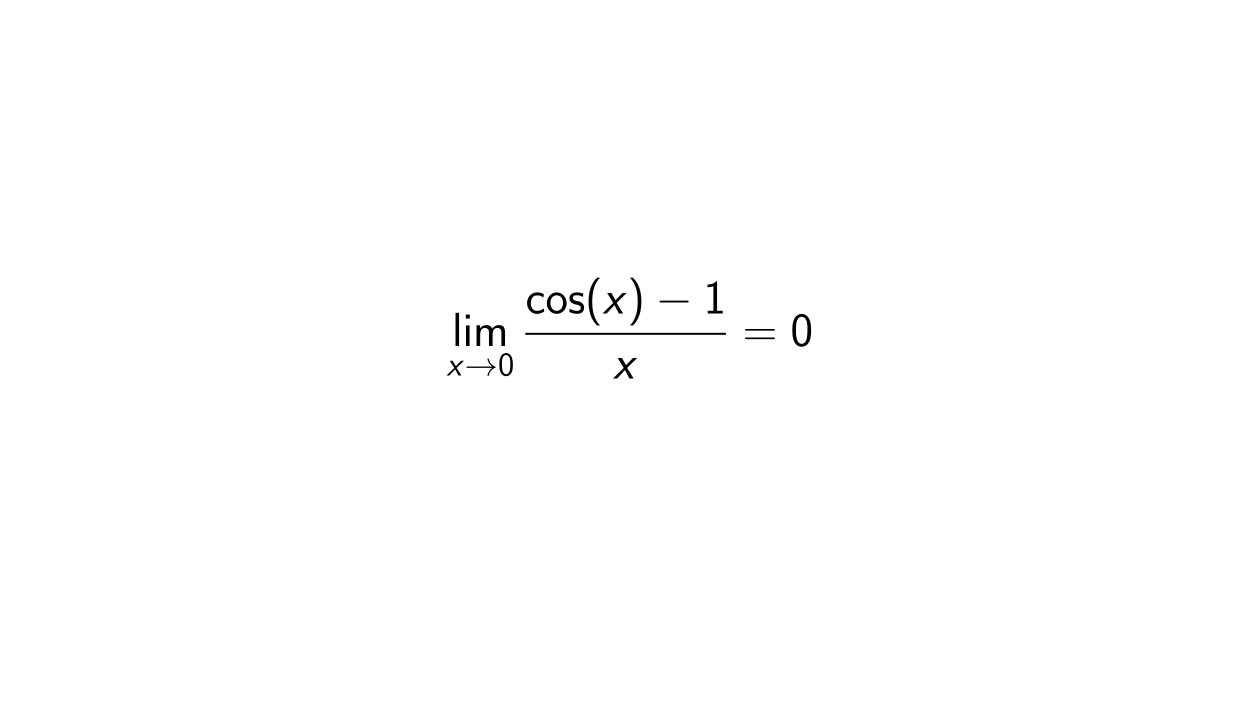Proof. We would like to prove the next limit:
\begin{equation*}
\lim_{x \rightarrow 0}\frac{\cos(x) - 1}{x} = 0
\end{equation*}\begin{equation*}
\cos(x) = 1 - 2\sin^2(x/2)
\end{equation*}\begin{align*}
\lim_{h \rightarrow 0}\frac{\cos(x) - 1}{x} &= \lim_{x \rightarrow 0}\frac{- 2\sin^2(x/2)}{x} \\
&= \lim_{x \rightarrow 0}\frac{- 2\sin^2(x/2)}{x} \\
&= -\lim_{x \rightarrow 0}\frac{\sin(x/2)}{x/2} \cdot \lim_{x \rightarrow 0} sin(x/2) \\
&= (-1) \cdot 0 = 0.
\end{align*}\begin{align*}
\cos(x) &= \sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n)!}x^{2n} \\
&= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots
\end{align*}\begin{align*}
\lim_{x \rightarrow 0}\frac{\cos(x) - 1}{x} &= \lim_{x \rightarrow 0}\frac{- \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots}{x} \\
&= \lim_{x \rightarrow 0} - \frac{x}{2!} + \frac{x^3}{4!} - \cdots \\
&= 0
\end{align*}