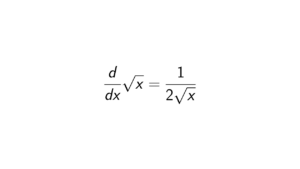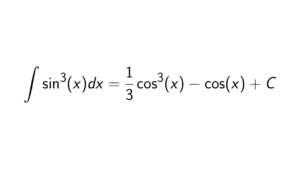Proof.
Associativity: let a,b,c \in \mathbb{Z}. Then
\begin{align*}
(a + b) + c = a + b + c = a + (b + c) \\
\end{align*}Identity: let a \in \mathbb{Z}. Then let e be an element of \mathbb{Z} such that a + e = e + a = a. Logically, this means that e = 0. So 0 is the identity element of \mathbb{Z} under addition.
Inverse: let a \in \mathbb{Z}. Then there exist an element a^{-1} such that a + a^{-1} = a^{-1} + a = e. We see that a^{-1} = -a and therefore -a is the inverse element of a.
We have proved all three properties; therefore, the ordered pair (\mathbb{Z}, +) is a group.
The set of integers is a commutative group too under addition. This is easy to verify.