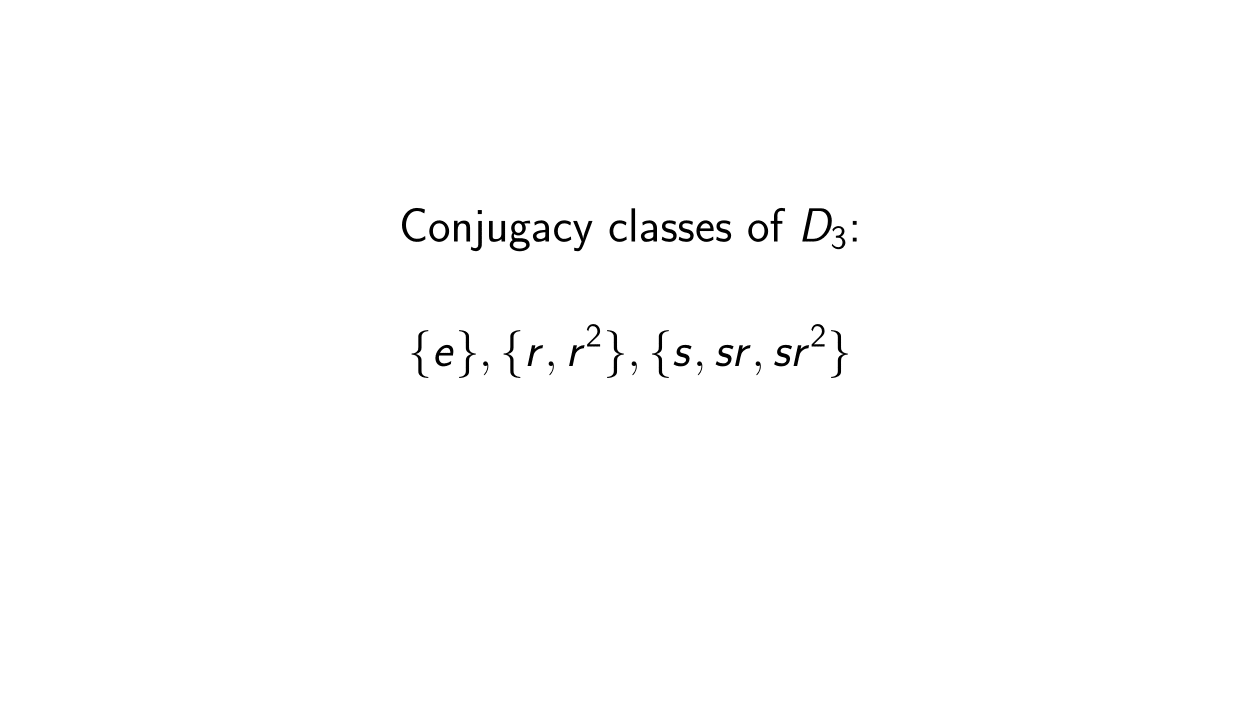The conjugacy classes of
D_3 are
\{e\} ,
\{r,r^2\} and
\{s,sr,sr^2\} . We know that
\begin{equation*}
D_3 = \langle r,s \ | \ r^3 = s^2 = e, rs = sr^{-1} \rangle
\end{equation*}
Some books may write it as
D_6 , but we prefer to take the
D_n instead of
D_{2n} . To determine the conjugates of the element
\tau \in D_3 , we need to show determine
\sigma \tau \sigma^{-1} for all
\sigma \in D_3 . So we will check one by one the conjugates of the elements of the dihedral group
D_3 :
\tau = e \begin{align*}
eee &= e \\
rer^{-1} &= e \\
r^2er^{-2} &= e \\
ses^{-1} &= e \\
rse(rs)^{-1} &= e \\
r^2se(r^2s)^{-1} &= e \\
\end{align*} \tau = r \begin{align*}
ere &= r \\
rrr^{-1} &= r \\
r^2rr^{-2} &= r^{2 + 1 - 2} = r \\
srs^{-1} &= srs = ssr^{-1} = r^{2} \\
rsr(rs)^{-1} &= rsrs^{-1}r^{-1} = sr^{-1}rs^{-1}r^{-1} = r^{-1} = r^{2} \\
r^2sr(r^2s)^{-1} &= rsr^{-1}rs^{-1}r^{-2} = r^{-1} = r^{2} \\
\end{align*} \tau = r^2 \begin{align*}
er^2e &= r^2 \\
rr^2r^{-1} &= r^2 \\
r^2r^2r^{-2} &= r^{2 + 2 - 2} = r^2 \\
sr^2s^{-1} &= sr^{-1}s^{-1} = rss^{-1} = r \\
rsr^2(rs)^{-1} &= rsr^2s^{-1}r^{-1} = rsr^2sr^{-1} = rsr^2rs = rss = r \\
r^2sr^2(r^2s)^{-1} &= r^2sr^{-1}s^{-1}r^{-2} = r^2rss^{-1}r^{-2} = r^{-2} = r \\
\end{align*} \tau = s \begin{align*}
ese &= s \\
rsr^{-1} &= sr^{-1}r^{-1} = sr \\
r^2sr^{-2} &= r^2sr = rs = sr^2 \\
sss^{-1} &= s \\
rss(rs)^{-1} &= r(rs)^{-1} = rsr^2 = sr \\
r^2ss(r^2s)^{-1} &= r^2sr^{-2} = sr^{-1} = sr^{2} \\
\end{align*} \tau = rs = sr^2 \begin{align*}
e(rs)e &= rs = sr^2 \\
r(rs)r^{-1} &= r^2sr^{-1} = s \\
r^2(rs)r^{-2} &= sr^{-2} = sr \\
s(rs)s^{-1} &= sr \\
rs(rs)(rs)^{-1} &= rs = sr^2 \\
r^2s(rs)(r^2s)^{-1} &= r^2srssr^{-2} = r^2sr^2 = s \\
\end{align*} \tau = r^2s = sr \begin{align*}
e(r^2s)e &= r^2s = sr \\
r(r^2s)r^{-1} &= sr^{-1} = sr^2 \\
r^2(r^2s)r^{-2} &= rsr^{-2} = s \\
s(r^2s)s^{-1} &= sr^2 \\
rs(r^2s)(rs)^{-1} &= rsr = s \\
r^2s(r^2s)(r^2s)^{-1} &= r^2s = sr \\
\end{align*}
We see, therefore, that we have the next conjugacy classes of
D_3 :
\begin{equation*}
\{e\}, \{r,r^2\}, \{s,sr,sr^2\}
\end{equation*}
You Might Also Like