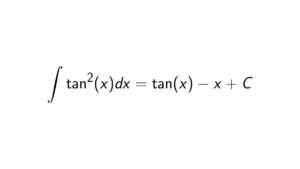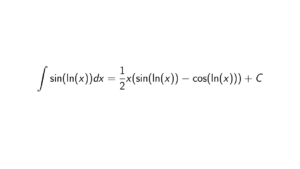Two ideals (a) and (b) in PID are comaximal iff gcd(a,b) = 1

How to prove that two ideals (a) and (b) in PID are comaximal iff gcd(a,b) = 1

The best way to tackle this problem is by using the definition of a comaximal.

Proof: let

R

be a PID. We will start with the right implication:

“ $\Rightarrow$ “: let $d$ be the generator for the principal ideal generated by $a$ and $b$ , i.e.,

\begin{equation*} (d) = (a,b) = \{ax+by \ | \ x,y\in R\}. \end{equation*}

We have given that

(a) + (b) = R

since

(a)

and

(b)

are comaximal. So this means that

1 \in (a) + (b)

and therefore we have an

R

-linear combination

ax + by = 1

for some

x,y\in R

. This means that

gcd(a,b) = 1

since

ax + by \in (a,b)

“ $\Leftarrow$ “: reverse the previous proof.