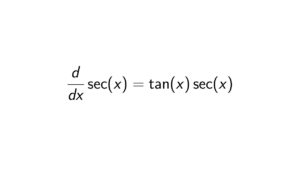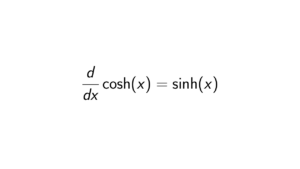Blog

Every infinite cyclic group is isomorphic to the additive group of Z

We will prove that every infinite cyclic group is isomorphic to the additive group of Z.

Define the following mapping: 
\begin{align*}
f: \mathbb{Z} &\longrightarrow \langle x \rangle \\
k &\longmapsto x^k,
\end{align*}
where \langle x \rangle is the infinite cyclic group. Then this map is isomorphic.

Proof. To prove that the map f is isomorphic, we need to show that f:
  • it is well defined,
  • is injective,
  • is surjective,
  • and is a homomorphism.
Well defined. The map is already well defined since there is no ambiguity in the representations of elements in the domain. To be more clear with an example, 2 = \frac{2}{1} = \frac{4}{2} etc, but \frac{2}{1},\frac{4}{2} \not \in \mathbb{Z}. So all elements in \mathbb{Z} are distinct. Same holds for \langle x \rangle since it is an infinite cyclic group.

Injectivity. All elements are distinct from what we have seen before, so if x^a \neq x^b, then a \neq b.

Surjectivity. The element x^k of \langle x \rangle is the image of k under f, so f is surjective.

Homomorphism. To prove that f is a homomorphism, we have done that here. Now we have shown that every infinite cyclic group is isomorphic to the additive group of Z.
Tags: ,

Leave a Reply