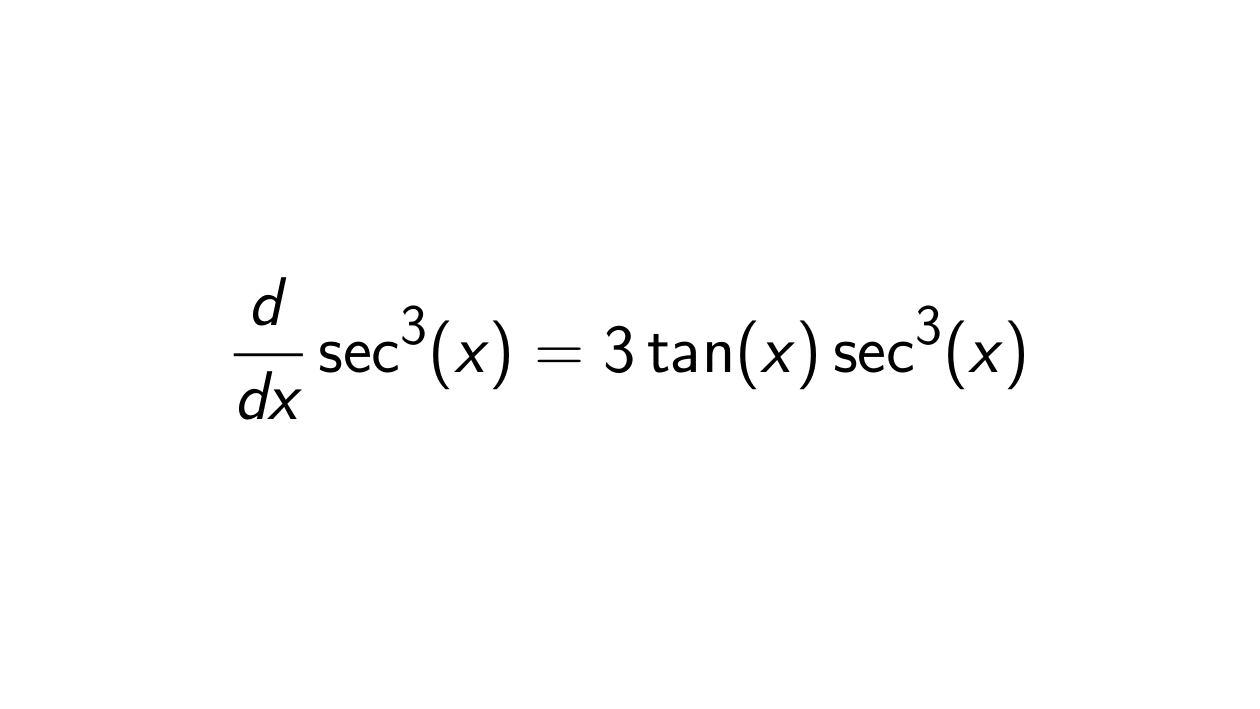What is the derivative of \sec^3(x)?
The derivative of
\sec^3(x) is
3\tan(x)\sec^3(x).
Solution of the derivative of \sec^3(x).
Let
F(x) = f(g(x)) = \sec^3(x), where
f(u) = u^3 and
g(x) = \sec(x). Then to determine the derivative of
\sec^3(x), we need to apply the chain rule:
\begin{align*}
F'(x) = f'(g(x))g'(x).
\end{align*}
It is easy to see that
f'(u) = 3u^2 and we have seen
here that
g'(x) = \tan(x)\sec(x). So we get:
\begin{align*}
f'(g(x)) = f'(\sec(x)) = 3\sec^2(x) \quad \text{and} \quad g'(x) = \tan(x)\sec(x).
\end{align*}
Substituting everything, we get:
\begin{align*}
F'(x) &= f'(g(x))g'(x) \\
&= 3\sec^2(x)\tan(x)\sec(x) \\
&= 3\tan(x)\sec^3(x).
\end{align*}Conclusion
So, the derivative of
\sec^3(x) is
3\tan(x)\sec^3(x).